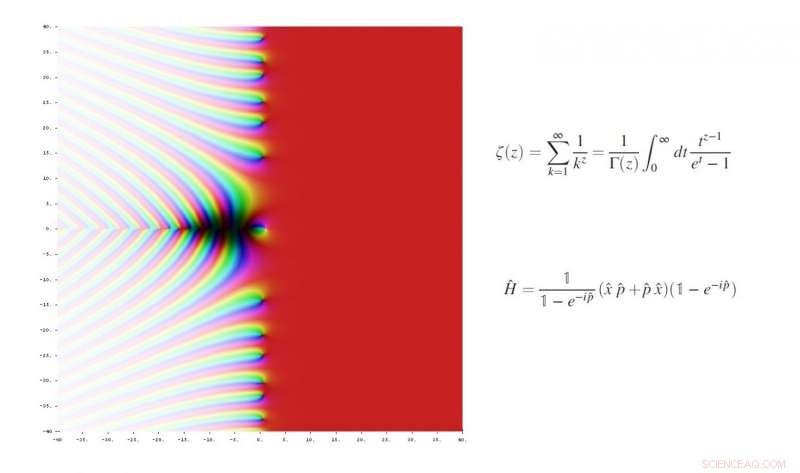
År 1859, Riemann antog att de otrivliga nollorna i Riemann zeta -funktionen ligger på den vertikala linjen (½ + it) på det komplexa planet, där den verkliga delen alltid är ½. Upphovsman:Jan Homann, Wikimedia Commons. Överst:Riemann zeta -funktion. Nederst:Den nya operatörsfunktionen.
(Phys.org) - Forskare har upptäckt att lösningarna på en berömd matematisk funktion som kallas Riemann zeta -funktionen motsvarar lösningarna från en annan, olika slags funktioner som kan göra det lättare att lösa ett av de största problemen i matematik:Riemann -hypotesen. Om resultaten kan verifieras noggrant, då skulle det äntligen bevisa Riemann -hypotesen, som är värt $ 1, 000, 000 Millennium Prize från Clay Mathematics Institute.
Medan Riemann -hypotesen går tillbaka till 1859, Under de senaste 100 åren har matematiker försökt hitta en operatörsfunktion som den som upptäcktes här, eftersom det anses vara ett viktigt steg i beviset.
"Så vitt vi vet, detta är första gången som en explicit - och kanske förvånansvärt relativt enkel - operatör har identifierats vars egenvärden ['lösningar' i matristerminologi] exakt motsvarar de icke -privata nollorna i Riemann zeta -funktionen, "Dorje Brody, en matematisk fysiker vid Brunel University London och medförfattare till den nya studien, berättade Phys.org .
Det som återstår att bevisa är det andra viktiga steget:att alla egenvärden är reella tal snarare än inbillade. Om framtida arbete kan bevisa detta, då skulle det äntligen bevisa Riemann -hypotesen.
Brody och hans medförfattare, matematiska fysiker Carl Bender från Washington University i St. Louis och Markus Müller vid University of Western Ontario, har publicerat sitt arbete i ett nyligen utgåva av Fysiska granskningsbrev .
Avstånd mellan primtal
Riemann -hypotesen har en så stark lockelse eftersom den är djupt kopplad till talteori och, särskilt, primtalen. I hans 1859 -papper, Den tyska matematikern Bernhard Riemann undersökte fördelningen av primtalen - eller mer exakt, problemet "givet ett heltal N, hur många primtal är det som är mindre än N? "
Riemann gissade att fördelningen av primtalen som är mindre än N är relaterad till de nontriviella nollorna i det som nu kallas Riemann zeta -funktionen, ζ ( s ). (Nollorna är lösningarna, eller värdena på s som gör funktionen lika med noll. Även om det var lätt för matematiker att se att det finns nollor när som helst s är ett negativt jämnt tal, dessa nollor anses vara triviala nollor och är inte den intressanta delen av funktionen.)
Riemanns hypotes var att alla nontriviala nollor ligger längs en enda vertikal linje (½ + den ) i det komplexa planet - vilket betyder att deras verkliga komponent alltid är ½, medan deras imaginära komponent i varierar när du går upp och ner på linjen.
Under de senaste 150 åren har matematiker har hittat bokstavligen biljoner nontriviala nollor, och alla har en realkomponent på ½, precis som Riemann trodde. Det är allmänt trott att Riemann -hypotesen är sann, och mycket arbete har gjorts baserat på detta antagande. Men trots intensiva ansträngningar, Riemanns hypotes - att alla de oändligt många nollorna ligger på denna enda rad - har ännu inte bevisats.
Identiska lösningar
En av de mest användbara ledtrådarna för att bevisa Riemann -hypotesen har kommit från funktionsteori, som avslöjar att värdena för den imaginära delen, t , där funktionen försvinner är diskreta tal. Detta tyder på att de icke -privata nollorna bildar en uppsättning verkliga och diskreta tal, vilket är precis som egenvärdena för en annan funktion som kallas en differentialoperator, som ofta används inom fysiken.
I början av 1900 -talet, denna likhet ledde till att vissa matematiker undrade om det verkligen finns en differentialoperator vars egenvärden exakt motsvarar nontriviala nollor i Riemann zeta -funktionen. Idag kallas denna idé för Hilbert-Pólya-gissningen, uppkallad efter David Hilbert och George Pólya - trots att ingen av dem publicerade något om det.
"Eftersom det inte finns någon publikation av Hilbert eller Pólya, det exakta uttalandet i Hilbert-Pólya-programmet kan i viss utsträckning tolkas, men det är förmodligen inte orimligt att säga att den består av två steg:(a) hitta en operatör vars egenvärden motsvarar de icke -privata nollorna i Riemann zeta -funktionen; och (b) avgöra om egenvärdena är verkliga, Sa Brody.
"Huvudfokus för vårt arbete hittills har legat på steg (a), "sa han." Vi har identifierat en operatör vars egenvärden exakt motsvarar de icke -privata nollorna i Riemann zeta -funktionen. Vi börjar bara tänka på steg (b), och verkligen hur man tacklar denna utmaning. Oavsett om det blir svårt eller enkelt att fylla i de saknade stegen mot steg (b), vid denna tidpunkt kan vi inte spekulera - ytterligare arbete krävs för att få en bättre känsla av svårighetsgraden. "
Operatören
En av de intressanta sakerna med den nyupptäckta operatören är att den har nära band med kvantfysik.
År 1999, när matematiska fysiker Michael Berry och Jonathan Keating undersökte gissningen Hilbert-Pólya, de kom med en annan viktig gissning. Om en sådan operatör finns, de sa, då bör det motsvara ett teoretiskt kvantsystem med särskilda egenskaper. Detta kallas nu för Berry-Keating-gissningen. Men ingen har någonsin hittat ett sådant system innan nu, och detta är en andra viktig aspekt av det nya arbetet.
"Vi har identifierat ett kvantiseringsvillkor för Berry-Keating Hamiltonian, verifierar således i huvudsak giltigheten av Berry-Keating-gissningen, Sa Brody.
Hamiltonianer används ofta för att beskriva energin i fysiska system. Den nya operatören, dock, verkar inte beskriva något fysiskt system, men är snarare en rent matematisk funktion.
"Det kan vara en besvikelse, men en sådan Hamilton verkar inte representera fysiska system på något uppenbart sätt; eller åtminstone hittills hittade vi ingen indikation på att vår Hamiltonian motsvarar något fysiskt system, Sa Brody.
"Men man kan då fråga sig" varför publicera i PRL ? ' Svaret beror på att många av de tekniker som används för någon heuristisk analys i vårt papper som är suggestiva är lånade från tekniker för pseudo-hermitisk PT-symmetrisk kvantteori som utvecklats under de senaste 15 åren eller så. Den konventionella förståelsen av Hilbert-Pólya-gissningen är att operatören (Hamiltonian) ska vara hermitisk, och man kopplar detta naturligtvis till kvantteori där Hamiltonians konventionellt krävs att de är hermitiska. Vi föreslår en pseudo-hermitisk form av Hilbert-Pólya-programmet, vilket för oss verkar vara värt att utforska ytterligare. "
Verkliga lösningar
Nu är den största utmaningen som återstår att visa att operatörens egenvärden är reella tal.
I allmänhet, forskarna är optimistiska att egenvärdena faktiskt är verkliga, och i sin artikel presenterar de ett starkt argument för detta baserat på PT -symmetri, ett koncept från kvantfysiken. I grund och botten, PT-symmetri säger att du kan ändra tecknen på alla fyra komponenter i rymdtid (tre rymd- eller "paritetsdimensioner" och en tidsdimension), och, om systemet är PT-symmetriskt, då ser resultatet likadant ut som originalet.
Även om naturen i allmänhet inte är PT-symmetrisk, operatören som fysikerna konstruerade är. Men nu vill forskarna visa att denna symmetri går sönder. Som de förklarar i sitt papper, om det kan visas att PT -symmetrin är trasig för operatörens imaginära del, då skulle det följa att egenvärdena alla är reella tal, som slutligen skulle utgöra det efterlängtade beviset på Riemann-hypotesen.
Det anses allmänt att ett bevis på Riemann -hypotesen kommer att vara mycket användbart inom datavetenskap, särskilt kryptografi. Forskarna vill också avgöra vad deras resultat faktiskt kan betyda för att förstå mer grundläggande matematiska principer.
"Det vi har utforskat hittills innehåller små talteoretiska insikter; medan man kan förvänta sig att, med tanke på dess betydelse i talteori, alla försök som framgångsrikt gör framsteg med att fastställa Riemann-hypotesen skulle ge talteoretiska insikter, "Sade Brody." Naturligtvis behöver detta inte vara fallet alls, men ändå skulle det vara av intresse att undersöka om någon av de dynamiska aspekterna av det hypotetiska system som beskrivs av vår Hamiltonian kan vara kopplad till vissa talteoretiska resultat. I detta avseende, semi-klassisk analys av vår Hamiltonian skulle vara ett av nästa mål. "
© 2017 Phys.org