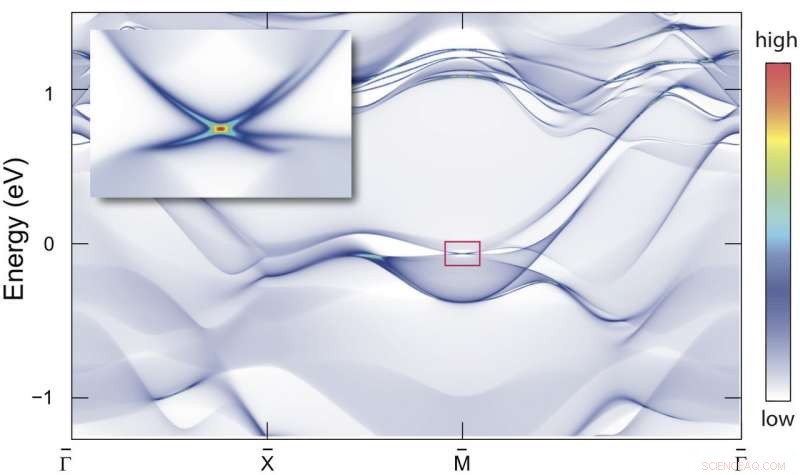
Ett nyidentifierat isolerande material som använder symmetriprinciperna bakom tapetmönster kan utgöra en grund för kvantberäkning, enligt ett internationellt team av forskare. Detta strontium-blyprov (Sr2Pb3) har ett fyrfaldigt Dirac-konytytillstånd, en uppsättning om fyra, tvådimensionella elektroniska yttillstånd som går bort från en punkt i momentumutrymmet i raka linjer. Upphovsman:Benjamin Wieder, Princeton University Institutionen för fysik
Ett internationellt team av forskare har upptäckt en ny, exotisk form av isolerande material med en metallisk yta som kan möjliggöra effektivare elektronik eller till och med kvantberäkning. Forskarna utvecklade en ny metod för att analysera befintliga kemiska föreningar som bygger på de matematiska egenskaperna som symmetri som styr de upprepande mönstren som ses i vardagliga tapeter.
"Det fina med topologi är att man kan tillämpa symmetriprinciper för att hitta och kategorisera material, "sa B. Andrei Bernevig, professor i fysik vid Princeton.
Forskningen, som visas den 20 juli i tidningen Vetenskap , involverat ett samarbete mellan grupper från Princeton University, University of Pennsylvania (Penn), Sungkyunkwan universitet, Freie Universität Berlin och Max Planck Institute of Microstructure Physics.
Upptäckten av denna form av bly-strontium (Sr 2 Pb 3 ) slutför en tioårig sökning efter ett svårfångat tredimensionellt material som kombinerar de unika elektroniska egenskaperna hos tvådimensionell grafen och tredimensionella topologiska isolatorer, en fas av materia som upptäcktes 2005 i oberoende verk av Charles Kane vid Penn och Bernevig i Princeton.
Vissa forskare har teoretiserat att topologiska isolatorer, som isolerar på insidan men leder elektricitet på ytan, kan fungera som en grund för supersnabb kvantberäkning.
"Du kan tänka på en topologisk isolator som en Hersheys kyss, "sa Kane, en motsvarande författare på tidningen. "Chokladen är isolatorn och folien är en ledare. Vi har försökt identifiera nya materialklasser där kristalsymmetrier skyddar den ledande ytan. Vad vi har gjort här är att identifiera den enklaste typen av topologisk kristallin isolator. "
Det nya verket visar hur symmetrierna hos vissa tvådimensionella ytor, känd som de 17 tapetgrupperna för sina tapetliknande mönster, begränsa det rumsliga arrangemanget (topologi) för tredimensionella isolatorer.
I en konventionell tredimensionell topologisk isolator, varje tvådimensionell yta uppvisar en enda karakteristisk grupp av tillstånd med konliknande dispersion. Dessa kottar liknar elementen på grafen som kallas Dirac -kottar, funktioner som genomsyrar materialet och andra tvådimensionella Dirac-halvmetaller med sina ovanliga elektroniska transportkvaliteter, men de är olika eftersom grafen har totalt fyra Dirac -kottar i två par som "limmas" ihop.
Kane hade misstänkt att med kristalsymmetrier, en andra typ av topologisk isolator kan existera med ett enda par limmade Dirac -kottar. "Vad jag insåg var att ett enda par Dirac-kottar är omöjliga i ett rent tvådimensionellt material, men det kan vara möjligt på ytan av en ny typ av topologisk isolator. Men när jag försökte bygga ett sådant tillstånd, de två kottarna kom alltid ogiltiga. "
En lösning uppstod när Benjamin Wieder, sedan en doktorand i Kanes grupp och nu en postdoktor i Princeton, besökte Princeton. I Princeton, Bernevig och kollegan Zhi Jun Wang hade just upptäckt "timglasisolatorer"-topologiska isolatorer med konstiga mönster av sammankopplade timglasliknande tillstånd-som Wieder kände igen som att du hade lindat en tredimensionell kristall med en speciell typ av mönstrad tapet.
"Vi insåg att du inte bara kunde få timglasisolatorn, men också denna speciella Dirac -isolator, genom att hitta en kristall som såg ut som den var täckt med rätt tapet, sa Wieder.
Särskilt, de insåg att ett limmat par Dirac -kottar kunde stabiliseras på kristallytor som har två skärande linjer längs vilka ytorna ser identiska ut efter att de vänds och vänds vinkelrätt. Dessa rader, känd som glidreflektioner, karakterisera de så kallade osymmorfa tapetgrupperna, och därmed ge namnet på denna nya fas, som laget kallade en "nonsymmorfisk Dirac -isolator."
Forskarna gick snabbt till jobbet med att tillämpa matematisk noggrannhet på Wieders inspiration, resulterar i en ny, tapet symmetri-baserad metodik för att diagnostisera bulk topologi av tredimensionella kristaller.
"Grundprinciperna är så enkla att vi skissade dem på servetter samma kväll, "sa medförfattaren Barry Bradlyn, en associerad forskare vid Princeton Center for Theoretical Science (PCTS).
"Men de är ändå tillräckligt robusta för att förutsäga och förstå en zoo av nya topologiska faser i verkliga material, "sa Wang, en postdoktor i fysik.
Upptäckten gjorde att forskarna direkt kunde relatera symmetrin hos en yta till närvaron av önskade topologiska yttillstånd för första gången, sa Penn's Andrew Rappe, en annan medförfattare på tidningen. "Detta möjliggör ett elegant och omedelbart användbart sätt att designa önskvärda yt- och gränssnittslägen."
För att identifiera Dirac -isoleringsfasen i naturen, forskarna beräknade de elektroniska strukturerna för hundratals tidigare syntetiserade föreningar med ytor med två glidlinjer (tapetgrupper pgg och p4g) innan de identifierade den nya topologin i bly-strontium.
Beräkningskemisterna "visste att de letade efter en nål i en höstack, men ingen brydde sig om att berätta för dem hur liten nålen kan vara, "sa Jennifer Cano, en associerad forskare vid PCTS.
När ännu mer exotiska topologiska isolatorer upptäcks, rollen som tapetgruppssymmetri, och det speciella, grafenliknande kottar i Dirac-isolatorn, har stelnat ytterligare.
"När du kan dela en sann yta Dirac-kon och samtidigt behålla tidsomvänd symmetri, något riktigt speciellt händer, "sa Bernevig." Du får tredimensionella isolatorer vars tvådimensionella ytor också är en slags topologisk isolator. "Sådana faser har nyligen förutsetts i vismutkristaller och molybden ditellurid (MoTe2) av flera medlemmar i samarbetet.
Vidare, med användning av en ny teori, topologisk kvantkemi, forskarna hoppas kunna hitta många fler av dessa exotiska faser.
"Om vi kunde måla dessa material med rätt tapeter, vi skulle se fler Dirac -isolatorer, "sa Wieder, "men ibland, fel tapet är också intressant. "