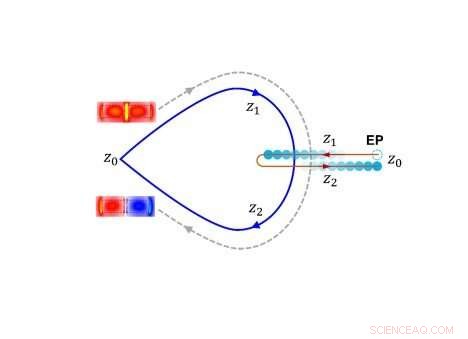
Lägesöverföring som vågledarnas geometriska parametrar omger en rörlig exceptionell punkt. Upphovsman:Wang Bing
Lägesstyrning är avgörande för optisk kommunikation och databehandlingsteknik. Oavsett om det är anslutningar och switchar i dataöverföringsledningar eller någon form av icke-ömsesidig enhet för optiska kretsar, förmågan att kontrollera, till exempel, om utmatningsläget kommer att vara jämnt eller udda för ett givet ingångsläge är nyckeln. Nu, forskare i Kina och Kanada har visat hur man kan uppnå effektiv överföring av optiskt läge i mer kompakta enheter än tidigare möjligt genom att utnyttja "exceptionella punkter" med nya mobila egenskaper.
"Det är alltid utmanande att uppnå sådana enheter med minimerad volym, låg införingsförlust, och hög effektivitet, "förklarar Bing Wang, en forskare vid Wuhan National Laboratory for Optoelectronics, Huazhong University of Science and Technology i Kina, och huvudförfattaren till rapporten om de senaste resultaten. För att hantera utmaningen, han och medarbetare vid Wuhan National Laboratory for Optoelectronics, Wuhan Institute of Technology, den kinesiska vetenskapsakademin Center for Excellence in Ultra-Intense Laser Science i Shanghai och University of Ottawa undersökte beteendet hos "exceptionella punkter"-ett matematiskt koncept som nyligen har väckt intresse för mikrovågsugn och optiska guidade system på grund av möjlig lägesöverföring med de topologiska egenskaper de beskriver.
Dock, tidigare ansträngningar att utnyttja exceptionella punkter i lägesöverföringsanordningar hindrades av begränsningar för att optimera lägesöverföringseffektiviteten och transmittansen, vilket oundvikligen resulterar i långa vågledare som inte är lämpliga för mer kompakta applikationer. För första gången, Wang och hans medarbetare övervägde möjligheten till exceptionella punkter som kan röra sig. Detta gjorde det möjligt för dem att uppnå höglägeöverföringseffektivitet och transmittans i en mycket kortare vågledare.
Vad är en exceptionell punkt?
Ett mångfald beskriver ett topologiskt utrymme som lokalt liknar det euklidiska utrymmet vid varje punkt. I verkligt endimensionellt utrymme, detta kan inkludera linjer eller cirklar, men inte åtta, eftersom övergångspunkten inte skulle hittas i det euklidiska rummet. Komplexa nummer inkluderar verkliga och imaginära delar, där den imaginära delen är proportionell mot kvadratroten av 1 och används ofta för att beskriva dämpningsbeteende i fysiska system. På grund av de två komponenterna, ett endimensionellt komplext grenrör presenteras som ett plan som kallas en Riemann-yta, som kan representera egenvärden för energin i ett visst läge i ett system med avledning. Den exceptionella punkten är den förgrenade singulariteten där två lägen möts, och detta är den topologiska egenskapen som tillåter lägeöverföring i systemet.
Wang och kollegor tillverkade vågledare med två galler som etsades i kisel på kiseloxid. Korrugeringarna vid gallerkanterna påverkar systemets effektiva förlust. Om tomter med gallerbredd och gallerseparation omger koordinaterna för exceptionella punkten, lägesöverföring sker, så en udda eller jämn lägesinmatning resulterar i en udda eller jämn lägesutgång beroende på systemparametrarna. Dock, antingen är den exceptionella punkten nära ingångsänden av vågledaren så att egenvärdena enkelt omger den för effektiv lägeöverföring, men transmittansen är låg på grund av den höga förlusten av systemet. Alternativt, den exceptionella punkten är långt från vågledarens ingång så att lägesöverföringseffektiviteten äventyras om inte vågledaren är mycket längre.
Flytta till spåret
Wang och kollegor kom runt avvägningen mellan vågledarlängd och prestanda genom att variera bredden och separationen av gallren, vilket gjorde att exceptionella punkter kunde röra sig. "Att flytta exceptionella punkter är ett begreppsgenombrott eftersom de ursprungligen betraktas i ett tvådimensionellt parameterutrymme, "förklarar Wang, som själv blev förvånad över hur tillvägagångssättet fungerade.
Faktiskt, han och hans kollegor hade fokuserat på att minska förlusten med stabila exceptionella punkter genom att ändra vågledarnas galler. "På det här sättet, dock, vi märkte att den exceptionella punkten inte längre är fixad, "Wang berättar för phys.org. Efter att ha utvecklat teorin för att förklara effekten, de kunde bekräfta sina resultat med numeriska simuleringar.
De förväntar sig att effekten är användbar för optiska omvandlare, kopplingar, filter och switchar i integrerade enheter, liksom optiska bredbandsisolatorer och cirkulatorer, som ger elektronisk-liknande riktningsförspänning till optiska kretsar. De anser också att det bör gälla akustiska och materiella vågor.
Nästa, de planerar att manipulera de exceptionella punkterna i realtid. LiNbO 3 har en stark elektrooptisk effekt, så att de kan manipulera vågledarens effektiva permittivitet genom att ändra ett externt elektriskt fält.
© 2020 Science X Network