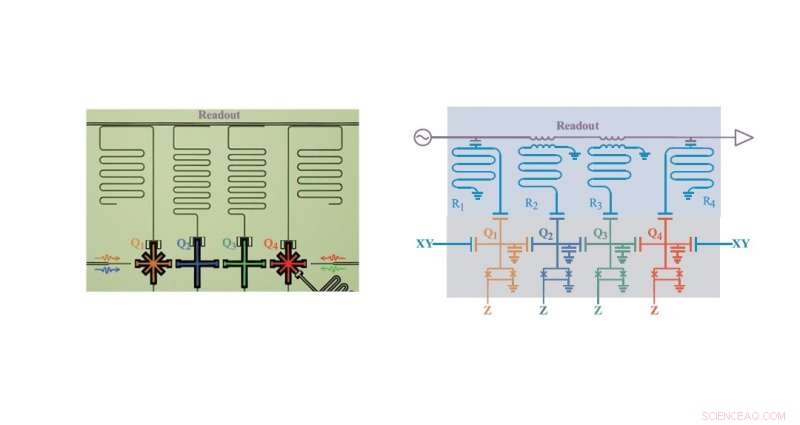
(Vänster) Falsk färgmikrofotografi och (höger) förenklat kretsschema för den superledande kvantkretsen för att lösa 2 × 2 linjära ekvationer. Metoden använder fyra qubits, märkt Q1 till Q4, med fyra motsvarande avläsningsresonatorer, märkt R1 till R4. Upphovsman:Zheng et al. © 2017 American Physical Society
(Phys.org) - Fysiker har experimentellt demonstrerat en rent kvantmetod för att lösa system av linjära ekvationer som har potential att arbeta exponentiellt snabbare än de bästa klassiska metoderna. Resultaten visar att kvantberäkning så småningom kan ha långtgående praktiska tillämpningar, eftersom lösning av linjära system vanligtvis sker inom vetenskap och teknik.
Fysikerna, ledd av Haohua Wang vid Zhejiang University och Chao-Yang Lu och Xiaobo Zhu vid University of Science and Technology of China, tillsammans med sina medförfattare från olika institutioner i Kina, har publicerat sin uppsats om vad de kallar en "quantum linear solver" i ett nyligen utgåva av Fysiska granskningsbrev .
"För första gången, vi har visat en kvantalgoritm för att lösa system av linjära ekvationer på en supraledande kvantkrets, "Berättade Lu Phys.org . "[Detta är] en av de bästa solid-state-plattformarna med utmärkt skalbarhet och anmärkningsvärd hög trovärdighet."
Kvantalgoritmen som de implementerade kallas Harrow, Hassidim, och Lloyd (HHL) algoritm, som tidigare visat sig ha förmågan, i princip, att leda till en exponentiell kvanthastighet över klassiska algoritmer. Dock, hittills har detta inte visats experimentellt.
I den nya studien, forskarna visade att en supraledande kvantkrets som kör HHL -algoritmen kan lösa den enklaste typen av linjärt system, som har två ekvationer med två variabler. Metoden använder bara fyra qubits:en ancilla qubit (en universell komponent i de flesta kvantdatasystem), och tre qubits som motsvarar ingångsvektorn b och de två lösningarna representerade av lösningsvektorn x i det linjära standardsystemet A x = b , där A är en 2 x 2 matris.
Genom att utföra en rad rotationer, byte av stater, och binära omvandlingar, HHL -algoritmen bestämmer lösningarna för detta system, som sedan kan avläsas med en kvantmätning utan mätning. Forskarna demonstrerade metoden med 18 olika ingångsvektorer och samma matris, skapa olika lösningar för olika ingångar. Som forskarna förklarar, det är för tidigt att säga hur mycket snabbare denna kvantmetod kan fungera eftersom dessa problem lätt kan lösas med klassiska metoder.
"Hela beräkningsprocessen tar ungefär en sekund, "Zhu sa." Det är svårt att direkt jämföra den nuvarande versionen med de klassiska metoderna nu. I det här arbetet, vi visade hur man löser det enklaste 2 x 2 linjära systemet, som kan lösas med klassiska metoder på mycket kort tid. Nyckelkraften för HHL -kvantalgoritmen är att, när man löser en 's-gles' systemmatris av mycket stor storlek, den kan få en exponentiell hastighet jämfört med den bästa klassiska metoden. Därför, Det skulle vara mycket mer intressant att visa en sådan jämförelse när storleken på den linjära ekvationen skalas till ett mycket stort system. "
Forskarna förväntar sig att i framtiden, denna kvantkrets skulle kunna skalas upp för att lösa större linjära system. De planerar också att ytterligare förbättra systemets prestanda genom att göra några enkla justeringar av enhetens tillverkning för att minska några av felen vid dess implementering. Dessutom, forskarna vill undersöka hur kretsen kan användas för att implementera andra kvantalgoritmer för en mängd olika storskaliga applikationer.
"Vår framtida forskning kommer att fokusera på att förbättra maskinvarans prestanda, inklusive längre sammanhållningstider, logikportar med högre precision, större antal qubits, lägre överhörning, bättre avläsningstrohet, etc., "Wang sa." Baserat på förbättringen av hårdvaran, vi kommer att demonstrera och optimera fler kvantalgoritmer för att verkligen visa kraften hos den superledande kvantprocessorn. "
© 2017 Phys.org