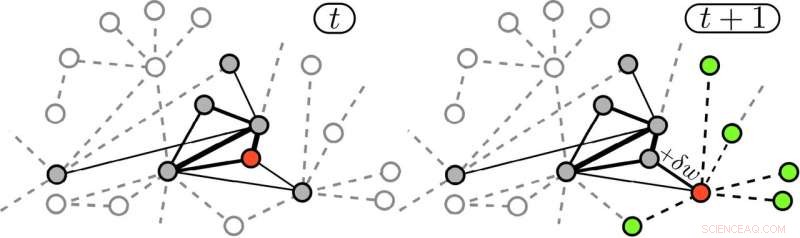
Kantförstärkta slumpmässiga promenader producerar en samutveckling av nätverket med dynamiken hos vandrare. Vid tidpunkten t är rullatorn på den röda noden och har redan besökt de grå noderna, medan de skuggade noderna fortfarande är outforskade. Kanternas bredd är proportionell mot deras vikt. Vid tidpunkten t + 1 har rullatorn flyttat till en närliggande nod (röd), och vikten av den använda kanten har förstärkts med δw. Vid denna tidpunkt, rullatorn går helst tillbaka, även om den också kan komma åt uppsättningen "angränsande möjliga" (grön). Kredit:Iacopo Iacopini
Forskare från Queen Mary University of London har utvecklat en matematisk modell för uppkomsten av innovationer.
Att studera kreativa processer och förstå hur innovationer uppstår och hur nyheter kan utlösa ytterligare upptäckter kan leda till effektiva interventioner för att främja framgång och hållbar tillväxt i samhället.
Empiriska rön har visat att det sätt på vilket nyheter upptäcks följer liknande mönster i en mängd olika sammanhang inklusive vetenskap, konst, och teknik.
Studien, publicerad i Fysiska granskningsbrev , introducerar ett nytt matematiskt ramverk som korrekt återger hastigheten med vilken nyheter uppstår i verkliga system, känd som Heaps lag, och kan förklara varför upptäckter är starkt korrelerade och ofta kommer i kluster.
Den gör detta genom att översätta teorin om det "angränsande möjliga", ursprungligen formulerad av Stuart Kauffman i samband med biologiska system, till språket i komplexa nätverk. Det intilliggande möjliga är uppsättningen av alla nya möjligheter som öppnar sig när en ny upptäckt görs. Nätverk har dykt upp som ett kraftfullt sätt att både undersöka verkliga system, genom att fånga de väsentliga relationerna mellan komponenterna, och att modellera den dolda strukturen bakom många komplexa sociala fenomen.
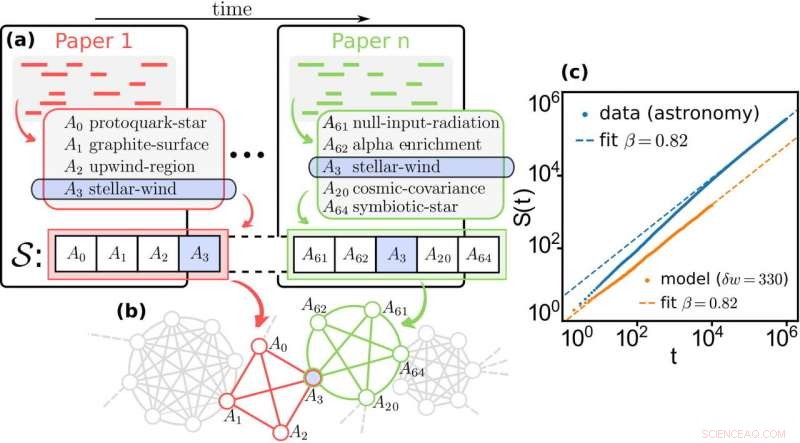
Kunskapstillväxt inom vetenskap. (a) En empirisk sekvens av vetenskapliga begrepp S extraheras från en tidsmässigt ordnad sekvens av artiklar genom att sammanfoga, för varje vetenskapsområde, de relevanta begreppen som finns i abstrakten. (b) Nätverket av relationer mellan begrepp konstrueras genom att länka alla begrepp som förekommer i samma abstrakt. Nätverket används sedan som en underliggande struktur för att köra vår kantförstärkta random walk-modell. (c) Modellen ställs sedan in på empiriska data genom att välja mängden förstärkning δw som reproducerar Heaps exponent β erhållen genom att anpassa Heaps kurva extraherad från S som en potenslag. Kredit:Iacopo Iacopini
I det här arbetet, nätverk används för att modellera det underliggande rummet av relationer mellan begrepp.
Huvudförfattare professor Vito Latora, från Queen Mary's School of Mathematical Sciences, sa:"Denna forskning öppnar nya riktningar för modellering av innovation, tillsammans med ett nytt ramverk som kan bli viktigt i utredningen av tekniska, biologisk, konstnärlig, och kommersiella system."
Han tillade:"Att studera processerna genom vilka innovationer uppstår kan hjälpa till att förstå huvudingredienserna bakom en vinnande idé, en banbrytande teknologi eller en framgångsrik kommersiell aktivitet, och är grundläggande för att ta fram effektiva datainformerade beslut, strategier, och insatser för att främja framgången och hållbar tillväxt i vårt samhälle."
I studien, upptäcktsprocessen är modellerad som en speciell klass av slumpmässiga vandringar, namngivna "förstärkta" promenader, på ett underliggande nätverk av relationer mellan koncept och idéer. En innovation motsvarar det första besöket av en webbplats i nätverket, och varje gång en rullator flyttar från ett koncept till ett annat, sådan association (en fördel i nätverket) förstärks så att den kommer att användas oftare i framtiden. Forskarna kallade detta den "kantförstärkta random walk"-modellen.
För att visa hur modellen fungerar i ett verkligt fall, de konstruerade också en datauppsättning av 20 år av vetenskapliga publikationer inom olika discipliner, såsom astronomi, ekologi, ekonomi och matematik för att analysera uppkomsten av nya begrepp. Detta visade att, trots sin enkelhet, den kantförstärkta random walk-modellen kan återge hur kunskap växer i modern vetenskap.
Professor Vito Latora tillade:"Ramverket vi presenterar utgör ett nytt tillvägagångssätt för studiet av upptäcktsprocesser, särskilt de för vilka det underliggande nätverket direkt kan rekonstrueras från empiriska data, till exempel användare som lyssnar på musik över ett likhetsnätverk mellan låtar. Vi arbetar redan med denna idé, tillsammans med en utökad version av vår modell, där vi studerar den kollektiva utforskningen av dessa nätverksbaserade utrymmen genom att överväga flera vandrare samtidigt."