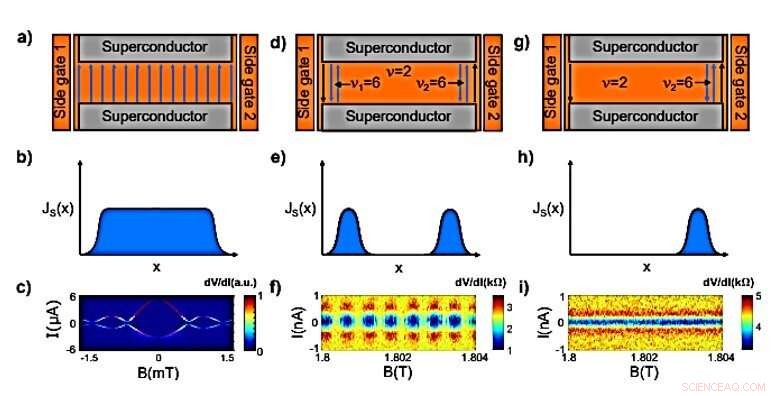
Tre kolumnjämförelse av överströmsfördelningarna och de resulterande magnetiska interferensmönstren. a) Diagram över superströmflöde vid låga magnetfält, vilket resulterar i en enhetlig fördelning som visas i panel (b). c) Mätning av den andra enheten vid lågt magnetfält som visar ett typiskt Fraunhofer -interferensmönster med en period på ∼ 0,7 mT, vilket indikerar en likformig superströmfördelning. Data är ett numeriskt derivat av de uppmätta IV-kurvorna (godtyckliga enheter). T =230 mK. d) Schematisk över QH -kanter när båda sidogrindarna appliceras (bulk ν =2, lokalt inducerad ν =6 på varje kant). De nära åtskilda motförökningsstaterna stöder superströmmar på båda kanterna av provet, vilket resulterar i fördelningen som visas i panel (e). Panelen (f) visar SQUID (supraledande kvantinterferensanordning) -liknande magnetiskt interferensmönster för quantum Halls överström motsvarande panel (d) med en periodicitet av ~ 0,6 mT. Panel (g) liknar panel (d) men med endast en sidogrind applicerad. Detta resulterar i att överströmmen bara flyter på en kant av provet, som visas i panel (h). Panelen (i) visar det magnetiska interferensmönstret som motsvarar panelen (g). Det finns ingen variation i mönstret på denna fältskala, anger en enda, mycket lokaliserad strömfördelning. Kredit:Science Advances, doi:10.1126/sciadv.aaw8693
I en ny rapport som publicerades den Vetenskapliga framsteg , Andrew Seredinski och medarbetare presenterade en grafenbaserad Josephson-korsning med dedikerade sidogrindar tillverkade av samma grafenark som själva korsningen. Det tvärvetenskapliga forskargruppen vid fysiska institutioner, astronomi och avancerat material i USA och Japan fann sidogrindarna vara mycket effektiva, tillåter dem att styra bärartätheten längs vardera kanten av korsningen över ett brett spektrum av magnetfält. Till exempel, de fyllde nästa Landau-nivå (där antalet elektroner är direkt proportionellt mot styrkan hos det applicerade magnetfältet) inom magnetfält i området 1 till 2-Tesla (T), att resultera i quantum Hall platåer. När de sedan introducerade motförökande kvant Hall-kanttillstånd längs vardera sidan av enheten, de observerade en superström lokaliserad längs kanten av korsningen. I det nuvarande arbetet, de studerade dessa superströmmar som en funktion av magnetfält och bärartäthet.
Inom kvantmekanik, fysiker klassificerar partiklar antingen som fermioner eller bosoner. Denna klassificering är avgörande för att förstå en mängd olika fysiska system, inklusive lasrar, metaller och superledare. Interaktioner mellan elektroner eller atomer i vissa tvådimensionella (2-D) system kan leda till bildning av kvasipartiklar som bryts från fermion-boson-dikotomin; att bilda 'icke-abeliska' tillstånd av materia. Många experimentella studier försöker identifiera icke-abeliska tillstånd i system som manifesterar quantum Hall (QH) effekter (kvantisering av motstånd i tvådimensionella elektroniska system). Identifieringen av sådana tillstånd kommer att vara användbar för kvantberäkning.
Fysiker förutspår samspelet mellan spin-spiralformade tillstånd och supraledning för att ge tillgång till icke-abelska excitationer som Majorana Zero-lägen (MZM). Dessa tillstånd kan utgöra grunden för kvantberäkningsarkitekturer, som utnyttjar topologiska skydd för att uppnå feltolerans, vilket gör att ett system kan fortsätta att fungera korrekt vid fel. Forskare siktar på att utveckla flera tekniker, inklusive hybrid superledare-halvledande nanotrådar och superledartopologiska isolatorstrukturer för sådana kvaspartikelbaserade applikationer. Nyligen forskningsintresse för supraledning hade också lett till ett flödande av aktivitet vid gränssnittet för supraledningsförmåga och kvant Hall (QH) -effekten. Till exempel, forskare har dragit slutsatsen att kvasi-endimensionella (1-D) supraledande kontakter kan möjliggöra MZM och parafermioner, medan heterostrukturer av grafen och hexagonal bornitrid (BN) med 1-D supraledande kontakter kan visa anmärkningsvärd kontakttransparens för att observera superström i QH-regimen. Dock, mikroskopiska detaljer om superström i QH -regimen förblir hittills ett öppet ämne.
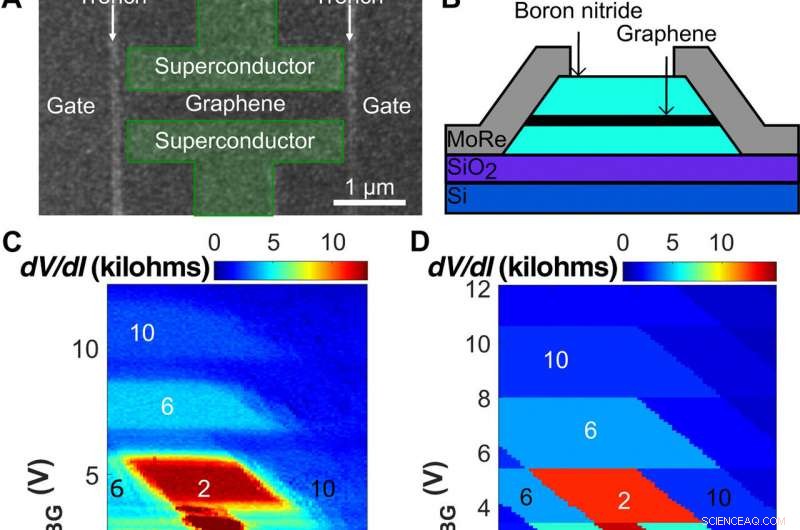
Enhetslayout och grindpåverkan på QH -platåer. (A) skanningselektronmikroskopi (SEM) mikroskop av enheten före reaktiv jonetsning. MoRe -kontakterna är konturerade och färgade gröna för kontrast. Två skyttegravar (ljusgrå), ~ 60 nm bred, separera korsningen från sidogrindarna. MoRe-kontakterna är åtskilda från skyttegravarna med ~ 100 nm breda områden av grafen, förhindra direkt kontakt mellan MoRe och kanten av mesan. (B) Schematisk sidovy av ett vertikalt tvärsnitt av (A). (C) Motståndskarta som en funktion av back-gate-spänning, VBG, och symmetriskt applicerade sidospänningar, VSG1 =VSG2, vid B =1,8 T. De diamantformade regionerna motsvarar platåerna med kvantiserat motstånd. Deras horisontella gränser (påverkas endast av VBG) motsvarar konstant elektrontäthet i massan. Diamanternas lutande sidogränser motsvarar konstanta fyllningsfaktorer nära kanterna, där påverkan av ryggen och sidogrindarna kompenserar varandra. De vita siffrorna markerar provets fyllningsfaktor, medan de svarta siffrorna vid den höga sidogrinden markerar provkonduktans i enheter på e2/h. (D) Elektrostatisk simulering av slutligt element av (C) reproducering av de diamantformade områdena med konstant konduktans. Konduktansplatåerna markerade i (C) är markerade på samma sätt. (E) Provmotstånd som funktion av VBG vid flera VSG1, 2, motsvarande vertikala tvärsnitt av (C). Kurvorna visar att QH -platåerna är bäst utvecklade med sidogrindarna inställda på -1 V. Vid VSG1, 2 =- 3 V och +1 V, platåerna krymper och blir asymmetriska mellan elektronen och hål-dopade sidor, som ofta finns i prover utan sidogatkontroll. Kredit:Science Advances, doi:10.1126/sciadv.aaw8693
I det nuvarande arbetet, Seredinski et al. undersökte en grafen Josephson -korsning med två grafensidportar för att direkt manipulera QH -kanttillstånd. De stämde in varje grind för att ändra fyllningsfaktorn för Landau -nivå längs kanterna för att observera en superström, endast lokaliserad längs ena kanten. Teamet byggde proverna från grafen inkapslad i hexagonal bornitrid (BN) för att skydda enheter från kontaminering och för att ge ballistisk transport över mikrometerskalor. De etsade grafen-BN-stacken och tillverkade sedan kvasi-1-D-kontakter till den exponerade regionen. De använde molybden rhenium (MoRe), en superledare av typ II och separerade de 3 µm breda kontakterna med 500 nm för att bilda den experimentella inställningen. I nästa steg, de bildade både korsningen och sidogrindarna genom att etsa smala skyttegravar på vardera sidan av kontakterna, för att effektivt kontrollera elektrontätheten längs korsningens kanter - efter att ha applicerat spänning på grafenregionerna. De överlappade inte de etsade skyttegravarna med kontakterna och placerade dem istället med en grafenlist, för att förhindra att elektroner tunnlar direkt från superledaren till kanten.
När Seredinksi et al. applicerade ett magnetfält vinkelrätt mot provet, korsningen gick in i QH (quantum Hall) -regimen. Med 1,8 Tesla, QH -effekten var mycket väl utvecklad och observerades med hjälp av resistenskartor som återges av en enkel elektrostatisk simulering i arbetet. Forskargruppen fick mer insikt i enhetens funktion genom att applicera sidogrindarna oberoende av varandra. De observerade sidogrindarnas inflytande på konduktanserna för att visa försumbar tvärprat mellan vänster port på höger kant, och vice versa. Forskarna ställde in portarna för att få ett QH-tillstånd att skapa motförökande tillstånd i enheten. Teamet observerade QH -superströmmen och dess interferensmönster som ett område med undertryckt motstånd flankerat av toppar; kännetecknande för en liten superström. Teamet reglerade enhetens funktioner för att lokalisera superströmmen till endera korsningen.
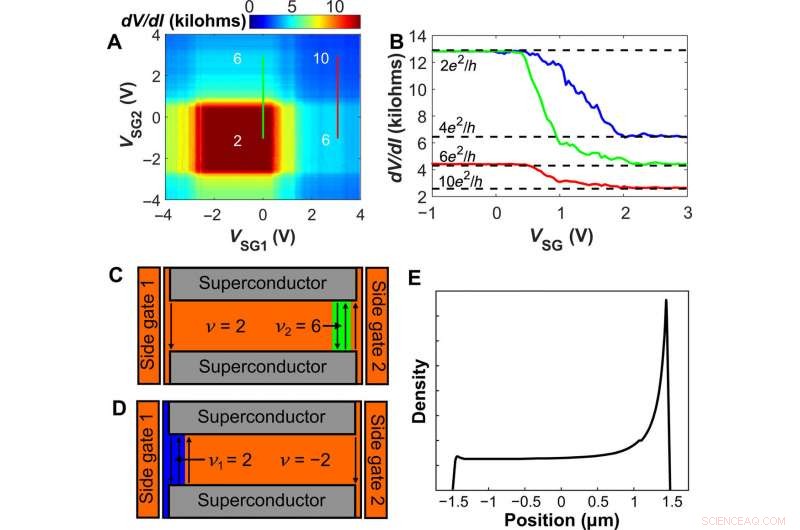
Sidogrind -inducerade QH -platåer. (A) dV/dI-kartan ritad kontra sidogatsspänningar VSG1 och VSG2 vid B =1,8 T. Bakspärrens spänning är fast vid VBG =4,7 V, motsvarande bulk -v =2 -tillståndet. Siffrorna markerar provkonduktansen i enheter av e2/h. (B) Provmotståndet mätt som en funktion av en enda sidogrind. Gröna och röda kurvor motsvarar de vertikala linjerna i (A) vid VSG1 =0 och 3 V, respektive (med VBG =4,7 V). Den blå kurvan visar ett liknande spår med en bulkfyllningsfaktor ν =- 2 (VBG =1,5 V), svepande VSG1 med VSG2 =0 V. (C och D) Scheman som motsvarar de gröna och blå kurvorna i (B) för VSG större än ∼2 V. Ytterligare kantkanaler skapas nära grinden, med lokal fyllningsfaktor ν2 =6 (C, grön region) och ν1 =2 (D, blå region). Ytterligare konduktans är lika med 4e2/h och 2e2/h i (C) och (D), respektive, ovanpå basledningen på 2e2/h, som observeras för de blå och gröna kurvorna i (B). (E) Schematisk över bärartätheten inom grafenkorsningen som en funktion av position när SG2 (1) är aktiv (passiv), besläktad med (C). Kredit:Science Advances, doi:10.1126/sciadv.aaw8693.
Superströmmen varierade inte för små förändringar i magnetfältet. Till exempel, när laget slog på en sidogrind, avståndet mellan de motförökande kantkanalerna i anordningen underlättade kopplingen av kanttillstånd till superledaren-för att överströmmen ska visas. När de applicerade båda sidor av portarna samtidigt, superströmens beroende av magnetfält förändrades helt. Den resulterande kartan visade ett supraledande kvantinterferensanordning (SQUID) -liknande interferensmönster. När Seredinski et al. utforskade enheten som en interferometer för QH -superströmmar, de ändrade fältet till 1 T för att observera en mer robust överladdningssignatur. De erhöll mönstret för motståndssvängningar i magnetfältet, där oscillationstiden var oberoende av grindspänningen, medan svängningsfasen varierade med porten.
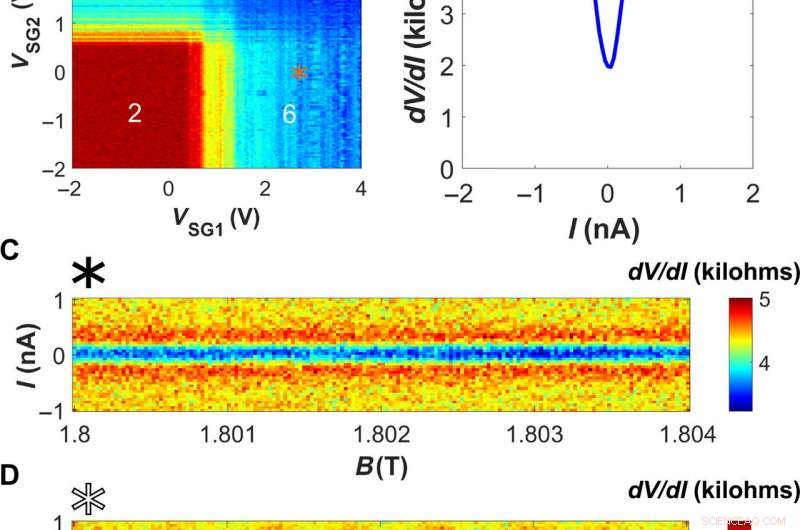
Superström QH och dess interferensmönster. (A) Differentialmotståndskarta kontra VSG1, 2 som i Fig. 2A men mätt med 0 nA DC -strömförspänning, tillåter observation av undertryckt motstånd på grund av överströmmen. Grindspänningsplatserna för (B) till (D) är markerade med (B) en orange asterisk, (C) en svart asterisk, och (D) en vit asterisk. (B) dV/dI uppmätt mot I, indikerar närvaron av en superström ovanpå den kvantiserade h/6e2 -platån. (C) Ström-magnetfältskarta över differentialmotståndet när en överström induceras längs ena sidan av provet endast med VSG2, medan VSG1 förblir på noll. Superströmmen är inte känslig för en inkrementell förändring av fältet på några milliteslas skala. (D) En liknande karta med båda sidogrindarna som inducerar superström, visar ett SQUID-liknande störningsmönster. Kredit:Science Advances, doi:10.1126/sciadv.aaw8693.
I ett ytterligare störningsmönster, forskargruppen observerade skillnaden i provmotståndet mellan 0 och 10 nanoampere (nA) DC -förspänning, för att markera de superledande regionerna. De mätte kartan som en funktion av båda sidogrindarna och observerade interferensen som motsvarar superströmmar som strömmar längs sidogrind-1 (SG1) och sidogrind-2 (SG2). De två portarna presenterade jämförbar effektivitet. När forskarna ökade spänningen i en grind, de minskade spänningen hos den motstående grinden för att ungefär behålla samma område av SQUID (superledande kvantinterferensanordning). Dessa områdesförändringar var tillräckliga för att utveckla skillnadsfasen över korsningen, även om det är för litet för att skapa märkbara förändringar i magnetfältets periodicitet.
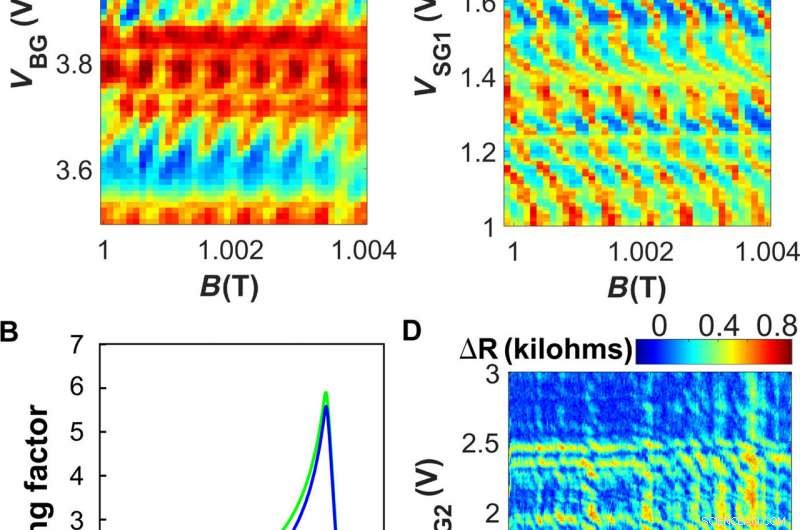
QH superström interferometri. (A) dV/dI -karta mätt vid VSG1 =2,34 V och VSG2 =2,36 V som en funktion av VBG och B nära 1 T. För en given grindspänning, regionerna med undertryckt motstånd motsvarar starkare superström. Oscillationernas fas beror på grindspänningen, indikerar att interferensområdet minskar med grindspänningen (positiv dVBG/dB). Detta förklaras av att de inre kanttillstånden rör sig längre inåt när elektrontätheten växer [schematisk i (B)]. (B) Schematisk bärartäthet i provet längs mittlinjen mellan kontakterna. Den blå linjen representerar en viss laddningstäthet vid baslinjen; den gröna linjen visar en högre back gate -spänning. (C) dV/dI -karta liknande (A) mätt som en funktion av B och SG1 spänning för VBG =3,8 V. Kartan visar ett interferensmönster med en lutning motsatt den i (A), indikerar att interferensområdet ökar med grindspänning när elektronerna skjuts längre mot grinden. (D) ΔR -karta som visar skillnaden mellan motståndet i 0 och 10 nA DC -förspänningsförhållanden, mätt vid 1 T med VBG =3,9 V. Båda sidogrindspänningarna är tillräckligt höga för att inducera en överström (VSG1, 2> 1 V), och de vertikala och horisontella funktionerna motsvarar överströmmen inducerad av SG1 eller SG2, respektive. Vid deras korsningar, ytterligare diagonala funktioner visas, indikerar störningar mellan superströmmarna på provets två sidor. Utkanterna har en lutning ∼ −1, vilket tyder på jämförbar effektivitet för de två sidogrindarna. Kredit:Science Advances, doi:10.1126/sciadv.aaw8693.
På det här sättet, Andrew Seredinski och kollegor visade inbyggda grafensidportar för att vara anmärkningsvärt effektiva för att kontrollera kanttillståndsutbredning i quantum Hall (QH) -regimen. De observerade superströmmar inducerade av sidogrindarna, ska bäras av QH -kanttillstånden. Dessa överströmmar flödade oberoende av varandra på varje kant av enheten och kunde styras oberoende av sina motsvarande grindar. Experimentet öppnar en lovande ny väg för att koppla superledare med QH-kanttillstånd för att få icke-abelska excitationer att ligga till grund för kvantberäkningsarkitekturer.
© 2019 Science X Network