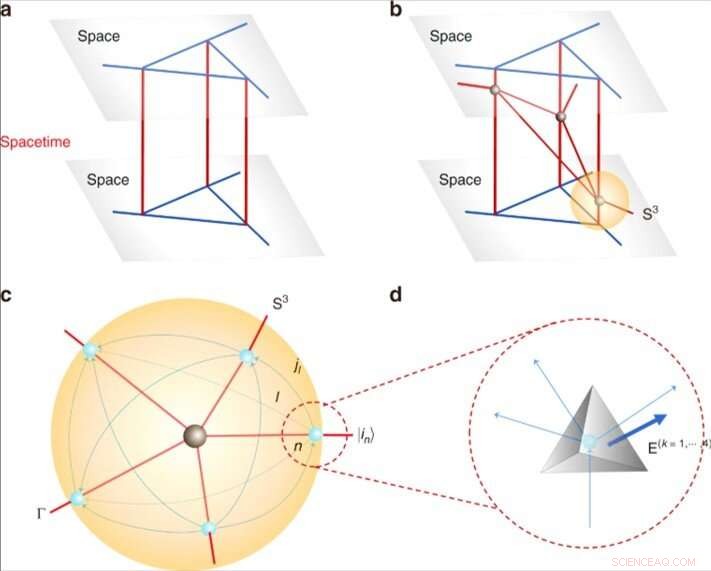
Kvantrumtid och tetraedrar. (a) En statisk 4d kvantrumtid från utvecklingen av spinnnätverket. (b) En dynamisk kvantrumtid med ett antal av fem valenta hörn (i svart) genom korsande världsark, varav en betecknas med S3. (c) Den lokala strukturen för en vertex från b genom att betrakta en 3-sfär S3 som omsluter vertexen. Skärningar mellan världsark och S3 ger ett spinnnätverk (i blått). Varje spinnnätverk representerar ett tillstånd |in⟩ och varje länk l är orienterad, som bär ett halvt heltal jl. (d) Kvantgeometriska tetraedrar. Varje nod i spinnnätverket representerar en kvanttetraeder. Att ansluta 2 noder med en länk i spinnnätverket motsvarar att limma 2 tetraedrar genom ansiktet dubbelt mot länken. Orienterade områden betecknas E(k=1, ⋯, 4)=(E(k)x, E(k)y, E(k)z). Kredit:Kommunikationsfysik, doi:10.1038/s42005-019-0218-5
Kvantsimulering spelar en oersättlig roll inom olika områden, bortom räckvidden för klassiska datorer. I en nyligen genomförd studie, Keren Li och ett tvärvetenskapligt forskarteam vid Center for Quantum Computing, Quantum Science and Engineering och Institutionen för fysik och astronomi i Kina, USA Tyskland och Kanada. Experimentellt simulerade spin-nätverkstillstånd genom att simulera kvantrumtidstetraedrar på en kvantsimulator med fyra qubit kärnmagnetisk resonans (NMR). Den experimentella troheten var över 95 procent. Forskargruppen använde kvanttetraedrarna framställda av kärnmagnetisk resonans för att simulera en tvådimensionell (2-D) spinfoam vertex (modell) amplitud, och visa lokal dynamik för kvantrumtid. Li et al. mätte de geometriska egenskaperna hos motsvarande kvanttetraedrar för att simulera deras interaktioner. Det experimentella arbetet är ett första försök och en grundläggande modul för att representera Feynman-diagrammets vertex i spinfoam-formuleringen, att studera loop quantum gravity (LQG) med hjälp av quantum information processing. Resultaten finns nu tillgängliga på Communication Physics.
Klassiska datorer kan inte studera stora kvantsystem trots framgångsrika simuleringar av en mängd olika fysiska system. De systematiska begränsningarna för klassiska datorer inträffade när den linjära tillväxten av kvantsystemstorlekar motsvarade den exponentiella tillväxten av Hilbertrymden, en matematisk grund för kvantmekaniken. Kvantfysiker siktar på att övervinna problemet med hjälp av kvantdatorer som bearbetar information i sig eller kvantmekaniskt för att överträffa sina klassiska motsvarigheter exponentiellt. 1982, Fysikern Richard Feynman definierade kvantdatorer som kvantsystem som kan styras för att efterlikna eller simulera beteendet eller egenskaperna hos relativt mindre tillgängliga kvantsystem.
I detta arbete, Li et al. använt kärnmagnetisk resonans (NMR) med en hög kontrollerbar prestanda på kvantsystemet för att utveckla simuleringsmetoder. Strategin underlättade presentationen av kvantgeometrier av rymd och rumtid baserat på analogierna mellan kärnspinntillstånd i NMR-prov och spinnnätverkstillstånd i kvantgravitation. Kvantgravitationen syftar till att förena Einsteingravitationen med kvantmekaniken för att utöka vår förståelse av gravitationen till Planckskalan (1,22 x 10) 19 GeV). På Planck-skalan (storlekar av rymden, tid och energi) Einsteins gravitation och kontinuumet av rumtidsnedbrytning kan ersättas via kvantrumtid. Forskningsmetoder för att förstå kvantrumstider är för närvarande rotade i spinnnätverk (en graf av linjer och noder för att representera rymdens kvanttillstånd vid en viss tidpunkt), som är viktiga, icke-störande ramverk av kvantgravitation.
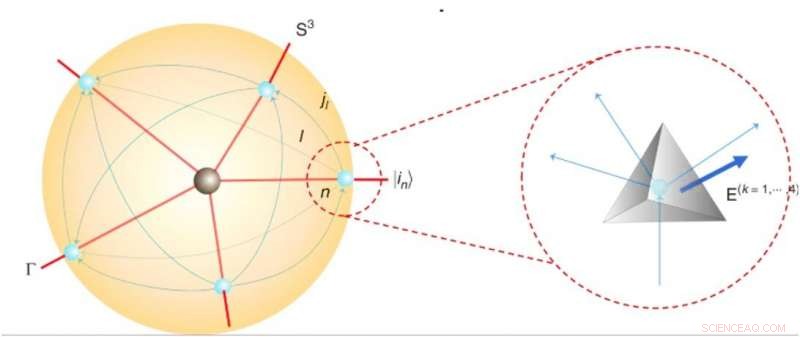
Kvantrumtid och tetraedrar inom ett spinnnätverk. Kredit:Kommunikationsfysik, doi:10.1038/s42005-019-0218-5
1971, fysikern Roger Penrose föreslog spinnnätverk motiverade av twistorteorin med efterföljande tillämpningar på loop quantum gravity (LQG). Spinnnätverken var kvanttillstånd som representerade i grunden diskreta kvantgeometrier av rymden på Planck-skalan. I föreliggande studie, forskargruppen representerade spinnnätverket med hjälp av en graf med länkar och noder färgade av spinhalvor. Till exempel, vilken nod som helst med kanter motsvarade en geometri och därför motsvarade en graf som innehöll fyravalenta noder kvanttetraedergeometri.
Forskargruppen utvecklade ett "nätverk" innehållande ett antal tredimensionella (3-D) världsark (2-D-ytor) och deras skärningspunkter. De visade att varje vertex där ytorna möttes, ledde till en kvantövergång som ändrade spinnnätverket för att representera kvantgeometrins lokala dynamik. Ungefär som Feynman-diagram (schematiska representationer av matematiska uttryck som beskriver beteendet hos subatomära partiklar), quantum spacetimes kodade övergångsamplituderna och spininfoam-amplituderna mellan de initiala och slutliga spinnnätverken. Kvantrymdtiderna och spininfoam-amplituderna som utvecklades i studien gav en konsekvent och lovande strategi för kvantgravitation. Li et al. presenterade NMR-simuleringen genom förmågan att kontrollera individuella qubits med hög precision. Kvanttetraedrarna och vertexamplituderna fungerade som byggstenar för LQG (loop quantum gravity) för att öppna ett nytt fönster för att inkludera LQG i kvantexperiment.
Forskarna härledde först ekvationer för att beskriva en kvanttetraeder inom ett spinnnätverk. I en schematisk 3+1-dimensionell dynamisk kvantrumtidsmodell, de demonstrerade en atom som en 3-sfär som omsluter en del av den kvantrymdtid som omger en vertex. Teamet modellerade gränsen för den inneslutna kvantrymdtiden precis som ett spinnnätverk och visade möjligheten att simulera stora kvantrumtider med många hörn genom att kvantlimma atomerna. Den resulterande strukturen liknade vertexamplitud av kvantrumtid liknande tidigare utvecklade Ooguris topologiska gittermodeller i fyra dimensioner. Forskarna visade LQG för att identifiera kvanttetraedergeometrier med kvantvinkelmomentet. Identifieringen gjorde det möjligt för dem att simulera kvantgeometrier med kvantregister (kvantmekanisk analog till ett klassiskt processorregister). I allmänhet, ett kvantregister kan uppnås matematiskt med hjälp av tensorprodukter.
UPP:Experimentellt preparerade tillstånd på Bloch-sfären och deras motsvarande klassiska tetraedrar. Tillstånden har formen cosθ2|0⟩L+eiϕsinθ2|1⟩L och är märkta med Ai, Bi, Ci, Di, Ei (i=0, 1), bland vilka, C0 och C1 är vanliga tetraedrar. |0L⟩ och |1L⟩ är bastillstånden i ett delrum av ett fyra-qubit-system, representerar en enda logisk qubit. NEDERST:Cosinusvärden för vinklar mellan ytnormaler i kvanttetraedern (cosinus för dihedriska vinklar skiljer sig med ett minustecken). Resultaten i experiment (teori) representeras av de färgade (transparenta) kolumnerna. Felstaplar kom från osäkerheten vid montering av kärnmagnetiska resonansspektra (NMR). Kredit:Kommunikationsfysik, doi:10.1038/s42005-019-0218-5 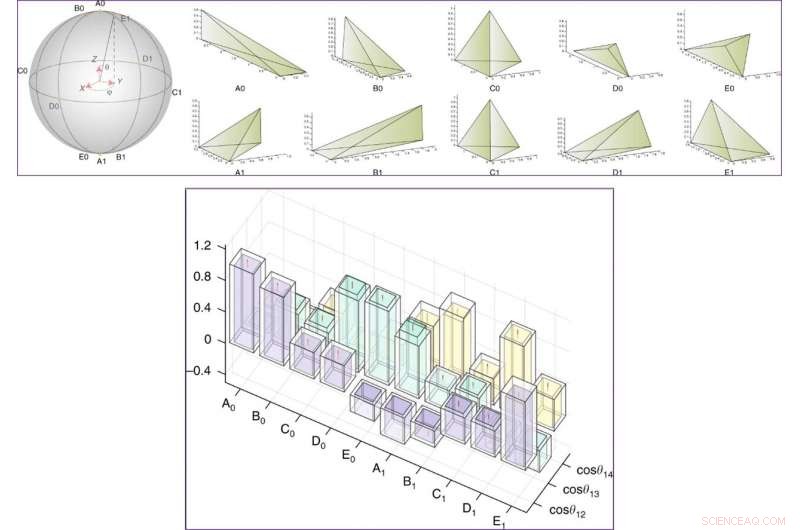
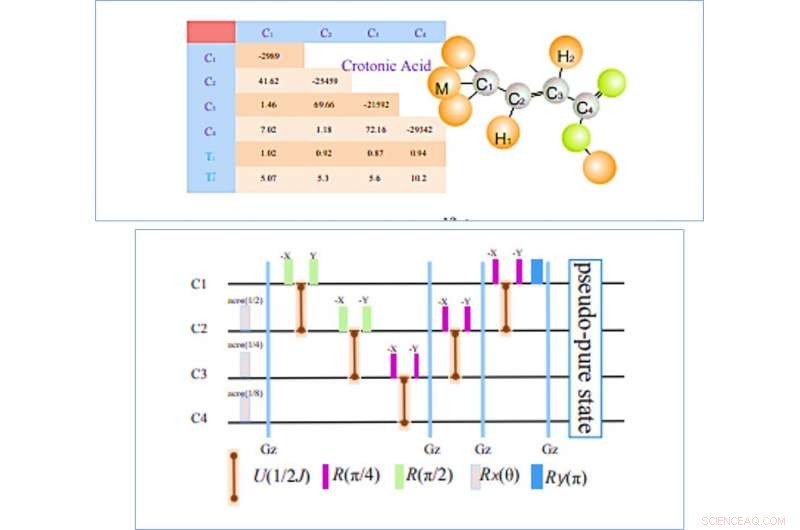
VÄNSTER:Krotonsyramolekylens struktur; De fyra 13C-kärnorna betecknas som de fyra qubitarna och tabellen till vänster visar parametrarna som konstruerar den inre Hamiltonian. Kemiska skift (Hz), J-kopplingsstyrkor (Hz) och relaxationstiderna (T1 och T2) är listade i den diagonala delen, off-diagonala element och botten, respektive. Alla parametrar mättes på en Bruker DRX 700 MHz spektrometer vid rumstemperatur. HÖGER:Pulssekvenser för att skapa det pseudo-rena tillståndet. Baserat på tekniken för rumslig medelvärde, kretsarna inkluderar lokal verksamhet, fem J-kopplingsutvecklingar, och fyra z-gradientpulser för att förstöra de oönskade koherenta termerna. varaktigheten av 1/2J fri utveckling beror på styrkan hos J-kopplingen mellan relevanta snurr. Kredit:Kommunikationsfysik, doi:10.1038/s42005-019-0218-5
För att erhålla vertexamplituderna, forskarna beräknade de inre produkterna mellan fem olika kvanttetraedertillstånd. Helst forskarna kunde ha använt en 20-qubit kvantdator, upprättande av två-qubit maximalt intrasslade tillstånd mellan två godtyckliga tetraedrar. Dock, eftersom en kvantdator av sådana dimensioner för närvarande är bortom kommersialiserad spjutspetsteknologi, forskarna genomförde växelvis fullständig tomografi av tillståndspreparatet för att få information om kvanttetraedertillstånd. När forskarna beräknade troheten mellan de experimentella kvanttetraedertillstånden och teorin, resultaten var långt över 95 procent. Med hjälp av kvanttetraedrarna, forskargruppen simulerade vertexamplituden. De jämförde resultaten mellan experimentet och den numeriska simuleringen bland alla fem tetraedrarna. Följaktligen, Sadelpunkter för amplituden i experimenten inträffade där de fem interagerande tetraedrarna visade en enkel geometrisk betydelse när de limmades för att bilda en geometrisk fyrsimplex.
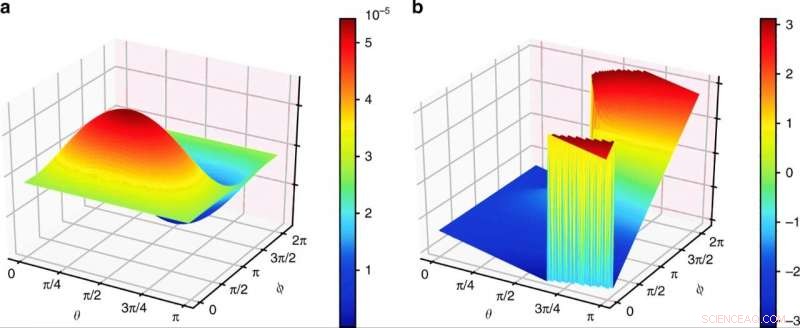
Resultaten av simulerade vertexamplituder a är amplituden av ekv. (3) och b beskriver informationen om dess fas. θ och ϕ är parametrarna för fyra qubits invariant-tensortillstånd som motsvarar de sfäriska koordinaterna på Bloch-sfären. Kredit:Kommunikationsfysik, doi:10.1038/s42005-019-0218-5
På det här sättet, Keren Li och medarbetare använde ett kvantregister i NMR-systemet för att skapa 10 invarianta tensortillstånd för att representera 10 kvanttetraedrar. De uppnådde en trohet över 95 procent och mätte därefter modellens dihedriska vinklar (två plana ytor). De övervägde spektrumpassningsfel och geometrisk identifiering för att förstå framgången med att simulera kvanttetraedrar i studien. Det nya forskningsarbetet presenterade ett första steg för att utforska spin-nätverkstillstånd och spininfoam-amplituder med hjälp av en kvantsimulator. Det medföljande arbetet visade också giltiga experiment för att studera LGQ.
© 2019 Science X Network