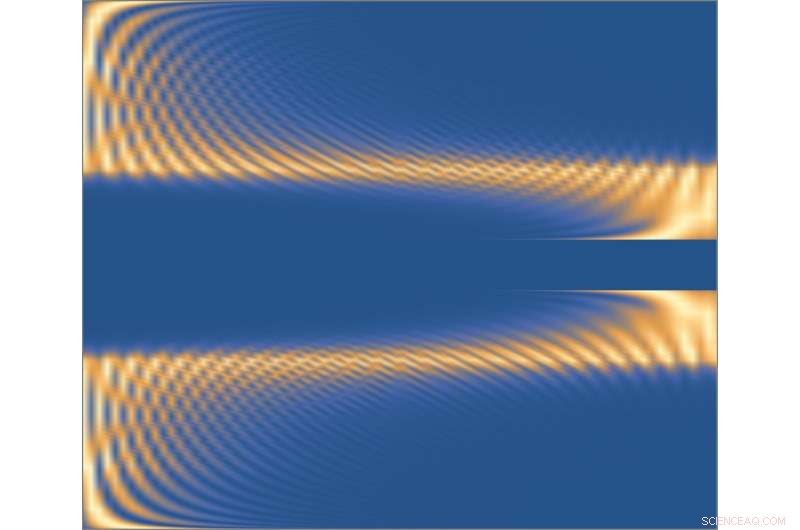
En figur som visar den "bipolära icke-hermitiska hudeffekten". Tillvägagångssättet för topologiska invarianter som utarbetats av forskarna är lätt att tillämpa även i närvaro av denna effekt. Kredit:Song, Yao och Wang.
I fysik, icke-ermitiska system är system som inte kan beskrivas med standard (d.v.s. Hermitiska) kvantmekanikens lagar, eller mer exakt, som bara kan beskrivas av icke-ermitiska Hamiltonianer. Icke-ermitiska system är allmänt förekommande i naturen. Många öppna system, dvs. system som inte är helt isolerade från resten av världen, tillhör denna klass. Topologin för dessa system (dvs. robusta egenskaper som är immuna mot alla förändringar av parametrar) är i grunden formad av den så kallade "icke-hermitiska hudeffekten, "som leder till okonventionell bulk-gränskorrespondens, som aldrig har observerats i hermitiska system.
Principen för bulkgränsöverensstämmelse skapar i huvudsak ett förhållande mellan en bulkegenskap hos ett material kodat i en topologisk invariant och vad som händer vid dess gräns (t.ex. på dess yta eller kanter). För att formulera denna bulkgränsöverensstämmelse, fysiker kräver en allmän och beräkningsbar definition av topologiska invarianter.
Än så länge, de flesta konstruktioner av icke-hermitiska topologiska invarianter har baserats på ett fint geometriskt objekt känt som den generaliserade Brillouin-zonen (GBZ), som först introducerades förra året av ett team av forskare vid Tsinghua University i Kina. Denna beräkning, dock, kan ibland vara mycket svårt att utföra (t.ex. för störda system), särskilt för mindre erfarna forskare.
För att övervinna denna begränsning, samma forskare som presenterade GBZ-beräkningen har nyligen kommit fram till en mer okomplicerad och användarvänlig konstruktion av topologiska invarianter. De presenterade detta nya tillvägagångssätt i en artikel publicerad i Fysiska granskningsbrev .
"Vi tar ett tillvägagångssätt med verkliga rymdvågfunktioner, som stimulerades av tidigare studier som utforskade hermitiska system av Alexei Kitaev och efterföljande verk av andra, "Zhong Wang, en av forskarna som genomförde studien, berättade för Phys.org. "Vid första ögonkastet, detta verkliga rymdtillvägagångssätt ser olämpligt ut för icke-hermitiska system på grund av det märkliga beteendet som kallas "icke-hermitiskt hudeffekt" hos icke-hermitiska system. Men någon gång, vi insåg att det kan fungera även i närvaro av icke-hermitisk hudeffekt. Verkligen, det gör det."
Det nya tillvägagångssättet för beräkning av topologiska invarianter som föreslås av Wang och hans kollegor innebär först beräkningen av ett systems vågfunktioner i det verkliga rummet, vilket är ett standardförfarande. När dessa vågfunktioner har beräknats, de icke-hermitiska topologiska invarianterna kan enkelt beräknas med hjälp av en serie formler som introducerats av forskarna.
En nyckelfunktion i denna nya konstruktion som föreslås av forskarna är att den kräver att man tar det så kallade "öppna gränsvillkoret". Faktiskt, det periodiska gränsvillkoret, som vanligtvis används när man studerar hermitiska system, skulle leda till ogiltiga resultat.
"Vår studie ger ett enkelt tillvägagångssätt för icke-hermitiska topologiska invarianter, och fördjupar också vår förståelse av den icke-hermitiska topologin, " Wang sa. "Detta tillvägagångssätt har flera fördelar. Först, det är användarvänligt; andra, den är allmänt användbar (t.ex. den kan tillämpas på slumpmässiga system där den generaliserade Brillouin-zonen inte är lätt att definiera)."
Det enkla och intuitiva tillvägagångssättet som introducerades av Wang och hans kollegor skulle kunna kasta lite ljus över några av de mest förvirrande aspekterna av icke-hermitisk topologi och icke-Bloch-bandteori. Deras konstruktion ger också övertygande bevis för att vissa säregna och ändå allmänna egenskaper hos icke-hermitiska system är, faktiskt, sant och naturligt.
I framtiden, teorin kan ha ett antal tillämpningar i den verkliga världen. Till exempel, det skulle kunna underlätta designen av högkvalitativa lasrar baserade på topologiska idéer.
"Vi arbetar nu med experimentella fysiker för att föra fler icke-ermitiska föreställningar till verklighet, " sa Wang. "Bland andra ansträngningar, vi undersöker den rika mångkroppsfysiken hos icke-hermitiska system, som för närvarande är dåligt förstådd."
© 2019 Science X Network