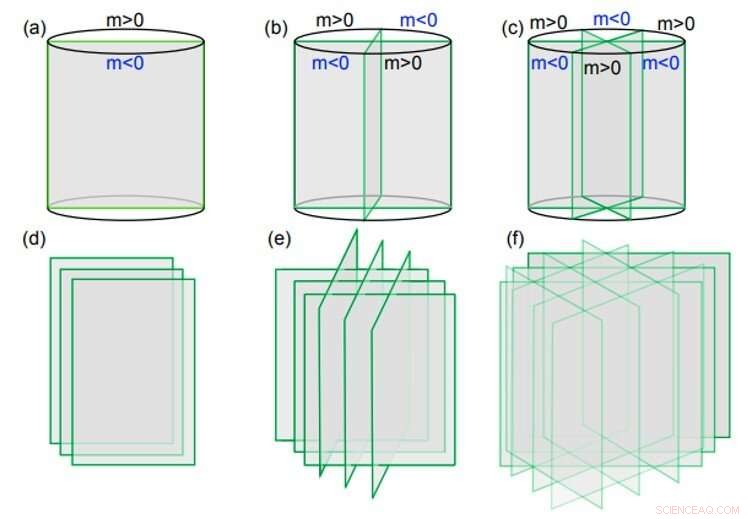
Real-space konstruktioner för C2, 4, 6-rotations- och tidsreverseringssymmetrier. (a-c) visa i frånvaro av översättningssymmetrier, de minimala konstruktionerna av dubbel, fyrfaldigt och sexfaldigt rotationssymmetriskyddade topologiska tillstånd i tre dimensioner, där varje plan är ett tvådimensionellt internt symmetriskyddat topologiskt tillstånd av antingen bosoner eller fermioner. Om det är en tvådimensionell topologisk isolator, de resulterande tillstånden är de topologiska kristallina isolatorerna som studeras i texten. (d-f) är enkla förlängningar av de minimala konstruktionerna, bygga tredimensionella modeller med translationssymmetri. Kredit:Science Advances, doi:10.1126/sciadv.aat2374.
I en ny rapport om Vetenskapens framsteg , Chen Fang och Liang Fu från Beijing National Laboratory for Condensed Matter Physics i Kina, Kavli institutet för teoretiska vetenskaper och institutionen för fysik, Massachusetts Institute of Technology i USA. Detaljerade upptäckten av nya typer av kvantanomalier i tvådimensionella system med tidsomkastande symmetri (T) (bevarande av entropi) och diskret rotationssymmetri; där en form bibehåller samma struktur efter rotation genom ett partiellt varv och ordning. De realiserade sedan fysiskt anomala tillstånd på ytan av nya klasser av topologiska kristallina isolatorer (TCI) vinkelräta mot rotationsaxeln och stöder ett spiralformigt läge. Närvaron av spiralformade lägen gjorde det möjligt för dem att bilda en ny kvantenhet från en topologisk kristallin isolator känd som en spiralformad nanorod med kvantiserad longitudinell konduktans.
En enda smak av masslös relativistisk fermion (elementarpartiklar) kan ha kvantanomalier där bevarandet av global symmetriström bryts på kvantnivå. Välkända exempel inkluderar den kirala anomalien hos Weyl-fermioner i tre dimensioner (3-D), och paritetsanomali i 2-D. I detta arbete, Fang och Fu presenterade en ny kvantanomali associerad med tidsomkastning (T) och diskret rotationssymmetri (C n =2, 4, 6). Sådana anomalier kunde bara existera i teorier som bröt kontinuerliga rotationssymmetrier i 2-D. Specifika material som TCI (topologiska kristallina isolatorer) kan vara värd för robusta yttillstånd som har en Dirac (grafenliknande) dispersion i förhållande till masslösa bärare. Att bryta skyddssymmetrin i sådana material kan göra att bärarna får massa.
Bildar nya klasser av TCI
I TCI, topologi och kristallsymmetri flätas samman för att bilda yttillstånd med distinkta egenskaper. Att bryta kristallsymmetri i TCI kan ge massa till masslösa Dirac-fermioner; därför, närvaron av topologiska yttillstånd skyddade av kristallsymmetrier är en definierande egenskap hos TCI. De 230 tidigare identifierade rymdgrupperna som beskriver alla möjliga kristallsymmetrier tillåter många olika klasser av TCI. Forskare hade tidigare funnit en klass av TCI skyddad av reflektionssymmetri i IV-VI-halvledare och en annan klass av TCI skyddad gemensamt av glidreflektion och tidsreverseringssymmetri i isolatorer med stora gap för att bilda experimentella "timglas"-fermioner, samtidigt som man teoretiserar flera andra klasser av TCI.

Schemat för de gaplösa tillstånden i två dimensioner som har rotations- och tidsomkastningssymmetrier. Det finns (A) två, (B) fyra, och (C) sex Dirac-koner, relaterade till varandra av två-, fyra-, och sexfaldiga rotationssymmetrier, respektive, i den första Brillouin-zonen. Konturerna är gränserna för de oföränderliga Brillouin-zonerna, längs vilken Berry-fasen kvantiseras till antingen noll eller π. Kredit:Science Advances, doi:10.1126/sciadv.aat2374.
Standardsökningsproceduren för att hitta topologiska material innebär att man beräknar bandstrukturen för ett visst material för att förstå de elektroniska tillstånden, mata sedan in denna information till en formel för att avslöja om materialet är topologiskt. Dessutom, den elektroniska bandstrukturen, känd som förhållandet mellan en elektrons energi och dess kvasi-momentum, kan avgöra om ett material är en metall eller en isolator. Forskare hade nyligen bevisat en teori för att förutsäga och experimentellt upptäcka sådana topologiska material. I detta arbete, därför, Fang et al. förutspådde en ny klass av TCI som gemensamt skyddas av n-faldig rotation och tidsomkastande symmetri för att uppvisa topologiska yttillstånd innehållande masslösa Dirac-koner på topp- och bottenytorna.
Förstå rotationsanomali
Studiet av anomali ledde dem till att teoretisera nya klasser av invarianta tidsomkastande (där de underliggande lagarna inte är känsliga för tidens riktning) TCI med C n =2, 4, 6 rotationssymmetri. Dessa TCI hade anomala yttillstånd på topp- och bottenytor. För varje ny klass av TCI, laget konstruerade motsvarande topologiska invariant i förhållande till Bloch-vågfunktioner i momentumrymden. Baserat på dimensionsreduktion (antal slumpmässiga variabler eller attribut som övervägs) och domänväggstillstånd (magnetiska strukturer med ändlig bredd som separerar områden med enhetlig magnetisering inom ett magnetiskt material), forskarna gav vidare en enhetlig real-space-förståelse av dessa TCI. De förutspådde flera material för att realisera de anomala yttillstånden skyddade av två- och fyrfaldiga rotationssymmetrier. Forskarna föreslog sedan en ny kvantenhet baserad på anomalierna, känd som "spiralstaven, " gjorts med hjälp av dessa nya TCI.
Två distinkta C2-bevarande pseudospin-strukturer. Pseudospinstrukturen längs lika energikontur för något E> 0, i effektiva Hamiltonians (A) h+(kx, ky) =kxσx + kyσy och (B) h−(kx, ky) =kxσx − kyσy. Det ses att den vänstra strukturen har kontinuerlig rotationssymmetri och att den högra inte har det; man ser också att den rätta strukturen fortfarande bevarar dubbelrotation. Kredit:Science Advances, doi:10.1126/sciadv.aat2374. 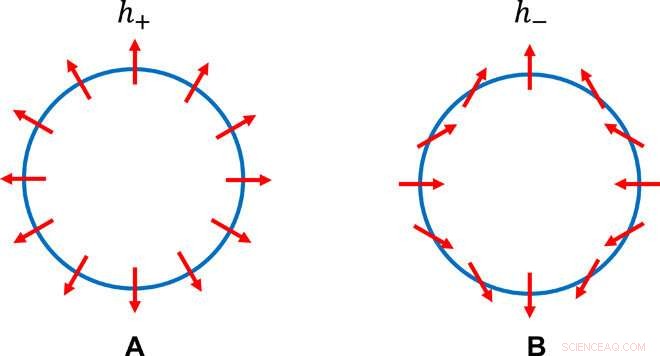
För att konstruera de nya TCI:erna och forma topologi i momentumrymden, Fang et al. skulle kunna lägga till två tidsomvändningsinvarianter (T-symmetri), starka topologiska isolatorer (TI) var och en med n-faldig rotationssymmetri. De övervägde den symmetri-tillåtna hybridiseringen mellan Dirac-fermionerna på ytan till TI:er för att erhålla de önskade yttillstånden för TCI:er. Forskarna beskrev Dirac-fermionerna med hjälp av h + och h - virvelliknande spinnstrukturer i momentumutrymme med vänster- och högerhänt chiralitet. Forskarna observerade närvaron och frånvaron av kontinuerlig rotationssymmetri genom att titta på pseudospin-vektormönstret på några lika energikonturer av h + och h - respektive.
Efter att ha etablerat TI-yttillståndsbandstrukturen, Fang et al. gav en alternativ förklaring av deras topologiska natur ur det verkliga rummets perspektiv, liknande en tidigare forskningsmetod. Real-space-metoden lade till symmetri-tillåtna störningar för att bryta translationssymmetri och gapa de masslösa Dirac-fermionerna på ytan för vidare studier. Fenomenen underlättade icke-triviala TCI-tillstånd och demonstrationer av deras robusthet under elektroninteraktioner. För detta, de ansåg en dubbel-TI-modell av en TCI placerad i en cylinder med en storlek större än korrelationslängden och ytan, slät på atomär skala. För C 4, 6 -TCI placerad på en cylinder, lägena för moderna på yttillstånden var inte fästa vid några fysiska gångjärn eller skärningspunkter mellan kristallina ytor. Även om den cylindriska formen innehöll kontinuerlig rotationssymmetri, systemet som beskrivs i studien bröt ner det till diskret rotationssymmetri, för att indikera förekomsten av 1-D gapfria linjer även på en perfekt atomisk slät cylinder.
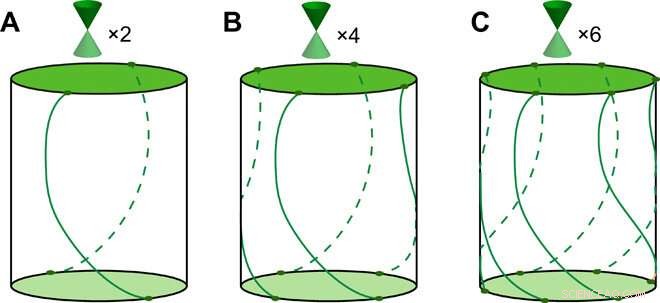
Ytans rotationstillstånd TCI. Schema över yttillstånd på över- och underytorna och kanttillstånden på de annars gapade sidoytorna av de nya TCI:erna skyddade av (A) dubbelt, (B) fyrfaldigt, och (C) sexfaldiga rotationssymmetrier i stavgeometrin. De övre och nedre ytorna har Dirac-koner, och på sidoytan, två, fyra, och sex spiralformade kantmoder förbinder de två ytorna; de kan ha godtycklig form och position men är relaterade till varandra genom två-, fyra-, och sexfaldiga rotationer, respektive. Kredit:Science Advances, doi:10.1126/sciadv.aat2374.
Fang et al. noterade sedan möjligheten att förstå topologiska kristallina tillstånd ur ett dimensionellt reduktionsperspektiv, där 3-D-tillståndet skulle kunna betraktas som en uppsättning av frikopplade lager av 2-D-topologiska tillstånd. Alla tre typer av nya TCI som introduceras i detta arbete skulle därför kunna konstrueras från 2D TI. Fang et al. använde denna konstruktion för att utöka sin teori om starkt interagerande symmetriskyddade topologiska tillstånd skyddade av rotationssymmetri och all lokal symmetri inklusive, men inte begränsat till tidsreverseringssymmetri.
Eftersom 1-D spirallägen är välkända för att vara fria från back-scatter på grund av tidsomkastande symmetri, denna unika egenskap tillät Fang et al. att designa en spiralformad nanorod från dessa nya material. Varje spiralform krävde bara tidsomkastningssymmetri för skydd och rotationssymmetrin säkerställde att de n-spiralformade moderna inte korsade varandra i verkligt utrymme och sprang ut. På det här sättet, så länge som rotationssymmetrin inte var avsevärt bruten, dessa spiralformade kantlägen skulle förbli stabila, även om de inte längre relaterade till varandra via en rotation - för att bilda nya klasser av TCI med ytrotationsanomali.
© 2020 Science X Network