
Upphovsman:CC0 Public Domain
Topologiska supraledare (TSC:er) är nya typer av topologiska kvanttillstånd med helt supraledande gapad bandstruktur i bulk, men de stöder gaplösa excitationer som kallas Majorana zero modes (MZM) vid gränserna. På grund av deras icke-lokala korrelation och icke-abeliska statistiska natur, MZM föreslås som qubits i topologisk kvantberäkning. Därav, sökning och drift av MZM:erna i TSC -material är nu ett viktigt ämne inom kondensmaterialets fysik.
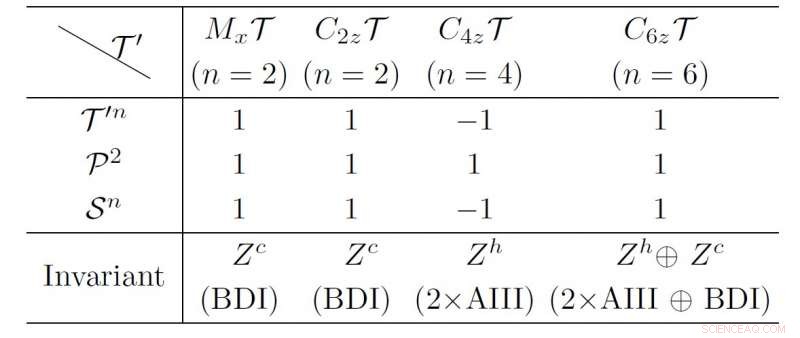
För att identifiera en TSC, man bör först fastställa dess topologiska klassificering. Den topologiska klassificeringen beror mycket på symmetrier inklusive tidsomvändningssymmetri, partikelhålssymmetri, och särskilt de kristallina symmetrier. Utan hänsyn till kristallina symmetrier, Bogoliubov-deGennes (BdG) Hamiltonians av 1-D-superledarna har bara Z2-klassificeringen. Spegelreflektionens symmetri och rotationssymmetrier kan förbättra klassificeringen till Z -klass. Ändå, den topologiska klassificeringen av superledare med allmänna magnetiska symmetrier är fortfarande en öppen fråga.
I en ny forskningsartikel publicerad i Beijing-baserade National Science Review , forskare från Huazhong University of Science and Technology i Wuhan, Kina, och Princeton University i New Jersey, USA föreslog metoden för att klassificera den topologiska superledande fasen genom att undersöka kompatibiliteten mellan olika MZM. Medförfattare Jinyu Zou, Qing Xie, Zhida Song och Gang Xu analyserade den topologiska klassificeringen av gapade supraledande ledningar med lokala magnetiska symmetrier (LMS). De fann att en effektiv BDI -klass TSC kan realiseras i M x T eller C 2z T invariant tråd. Anmärkningsvärt, de nya TSC -faserna kännetecknas av Zh invariant i C 4z T -fall och Zhoplus Zc invariant i C6zT -fall upptäcks.
Den topologiska klassificeringen av 1D -gapade supraledande system med LMS. Upphovsman:© Science China Press
I artikeln med titeln "Nya typer av topologiska superledare under lokala magnetiska symmetrier". Författarna fokuserar på 1D supraledande trådar med LMSs T '=M x T, C 2z T, C 4z T och C 6z T. "Funktionen av T 'förändrar inte elektronernas position. Därför verkar den på BdG Hamiltonian som en tidsomvändningsoperator". Att kombinera T 'och partikelhålssymmetri P leder till en kiral symmetri S =T'P. BdG Hamiltonian kan anta den diagonaliserade formen enligt den kirala symmetrin. Och MZM är egenstaterna för den kirala symmetrin S. Författarna finner "MZM:er som har kirala egenvärden s och -s kan kopplas till varandra och elimineras." Efter riktlinjen, de analyserar kompatibiliteten hos MZM:erna i slutet av 1D -supraledande ledningar med LMS, och sammanfatta deras topologiska klassificering enligt tabell I.
M x T och C 2z T -fall motsvarar BDI -klassen med kiral topologisk invariant Zc. Medan C4zT -fallet kännetecknas av spiralformad Z h oföränderlig, som indikerar flera Majorana Kramer -par i slutet av den supraledande tråden. I C 6z T -fall, "topologin för hela BdG Hamiltonian klassificeras av Z h oplus Z c , ". I en sådan ny topologisk fas, "spiralformade och kirala MZM kan samexistera."
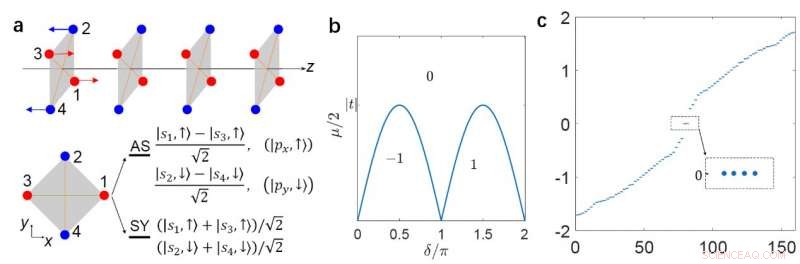
(a) En C4zT-bevarande supraledande tråd i linje med z-riktningen. (b) Det topologiska fasdiagrammet. c) spektrumet av icke -faslig fas med en öppen gräns på båda sidor, där fyra MZM visas med noll energi. Upphovsman:© Science China Press
"För att illustrera TSC -fasen med LMS C 4z T, vi konstruerar en 1D anti-ferromagnetisk kedja längs z-riktning, "tillägger forskarna. De ger modellens topologiska fasdiagram." I den icke -privata TSC -fasen, de öppna kvantrådarna fäller ett heltal par MZM i dess ändar. "de visar också MZM genom numerisk och analytisk beräkning.
"Dessa resultat berikar inte bara mångfalden av 1-D TSC, men också tillhandahålla frodiga byggstenar för konstruktion av nya typ 2-D och 3D-TSC "som de förutspår i slutet av artikeln, "Till exempel, man kan koppla 1D TSC:erna i y-riktning för att konstruera en 2-D TSC. De högsymmetriska linjerna ky =0 och ky =pi i momentumutrymmet bevarar 1D LMS. Med rätt parametrar, ky =0 och ky =pi linjer kan tillhöra distinkt topologisk fas, och resultera i de gaplösa utbredande Majorana -kanttillstånden som förbinder de ledande banden och valensbanden. "