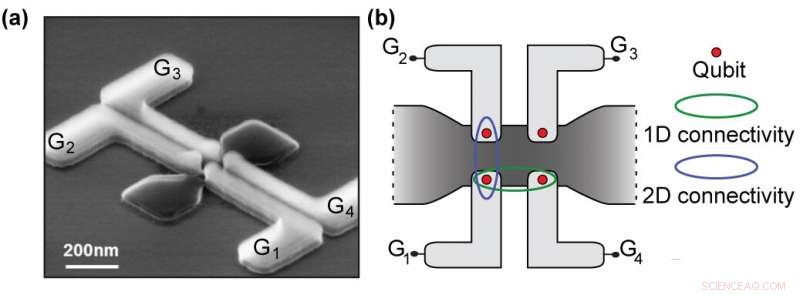
(a) Skanningselektronbild av en av de gjuteritillverkade kvantpunktpunkterna. Fyra kvantpunkter kan bildas i kisel (mörkgrå), med fyra oberoende styrtrådar (ljusgrå). Dessa ledningar är kontrollknapparna som möjliggör de så kallade kvantportarna. (b) Schematisk bild av den tvådimensionella matrisenheten. Varje Qubit (röd cirkel) kan interagera med sin närmaste granne i det tvådimensionella nätverket, och kringgå en Qubit som misslyckas av en eller annan anledning. Denna inställning är vad "andra dimensionen" betyder. Kredit:Köpenhamns universitet
Kvantdator:Ett av hindren för framsteg i jakten på en fungerande kvantdator har varit att de arbetsenheter som går in i en kvantdator och utför de faktiska beräkningarna, qubits, har hittills gjorts av universitet och i litet antal. Men under de senaste åren har ett paneuropeiskt samarbete, i samarbete med den franska mikroelektronikledaren CEA-Leti, har undersökt vardagstransistorer - som finns i miljarder i alla våra mobiltelefoner - för deras användning som qubits. Det franska företaget Leti gör gigantiska skivor fulla av enheter, och, efter mätning, forskare vid Niels Bohr Institute, Köpenhamns universitet, har funnit att dessa industriproducerade enheter är lämpliga som en qubit -plattform som kan flytta till den andra dimensionen, ett viktigt steg för en fungerande kvantdator. Resultatet publiceras nu i Naturkommunikation .
Quantum dots i tvådimensionell array är ett steg framåt
En av de viktigaste egenskaperna hos enheterna är den tvådimensionella uppsättningen kvantprickar. Eller mer exakt, ett två och två gitter av kvantprickar. "Det vi har visat är att vi kan realisera enstaka elektronstyrning i varenda en av dessa kvantpunkter. Detta är mycket viktigt för utvecklingen av en qubit, eftersom ett av de möjliga sätten att göra qubits är att använda snurrningen på en enda elektron. Så att nå detta mål att styra de enstaka elektronerna och göra det i en 2-D-uppsättning kvantpunkter var mycket viktigt för oss ", säger Fabio Ansaloni, tidigare doktorand studerande, nu postdoc i centrum för Quantum Devices, NBI.
Att använda elektronspinn har visat sig vara fördelaktigt för implementering av qubits. Faktiskt, deras "tysta" natur gör att snurr svagt interagerar med den bullriga miljön, ett viktigt krav för att få högpresterande qubits.
Att utvidga kvantdatorprocessorer till den andra dimensionen har visat sig vara avgörande för ett mer effektivt genomförande av kvantfelkorrigeringsrutiner. Kvantfelkorrigering gör det möjligt för framtida kvantdatorer att vara fultoleranta mot individuella qubitfel under beräkningarna.
Betydelsen av industriell skala produktion
Docent vid Center for Quantum Devices, NBI, Anasua Chatterjee tillägger:"Den ursprungliga idén var att göra en rad spin qubits, komma ner till enstaka elektroner och bli i stånd att styra dem och flytta runt dem. I den meningen är det riktigt bra att Leti kunde leverera de prover vi har använt, vilket i sin tur gjorde det möjligt för oss att uppnå detta resultat. Mycket kredit går till det paneuropeiska projektkonsortiet, och generös finansiering från EU, hjälper oss att långsamt flytta från nivån på en enda kvantpunkt med en enda elektron till att ha två elektroner, och går nu vidare till de tvådimensionella matriserna. Tvådimensionella matriser är ett riktigt stort mål, eftersom det börjar likna något du absolut behöver för att bygga en kvantdator. Så Leti har varit involverad i en rad projekt under åren, som alla har bidragit till detta resultat. "
Krediten för att komma så långt tillhör många projekt i hela Europa
Utvecklingen har gått gradvis. År 2015, forskare i Grenoble lyckades göra den första snurrqubit, men detta var baserat på hål, inte elektroner. Då, prestandan hos de enheter som tillverkades i "hålregimen" var inte optimal, och tekniken har avancerat så att enheterna nu vid NBI kan ha tvådimensionella matriser i den enda elektronregimen. Framstegen är trefaldiga, forskarna förklarar:"Först, att producera enheterna i ett industriellt gjuteri är en nödvändighet. Skalbarheten hos en modern, industriell process är avgörande när vi börjar göra större matriser, till exempel för små kvantsimulatorer. Andra, när man gör en kvantdator, du behöver en array i två dimensioner, och du behöver ett sätt att ansluta den yttre världen till varje qubit. Om du har 4-5 anslutningar för varje qubit, du hamnar snabbt med ett orealistiskt antal ledningar som går ut från lågtemperaturinställningen. Men det vi har lyckats visa är att vi kan ha en grind per elektron, och du kan läsa och styra med samma grind. Och till sist, med dessa verktyg kunde vi flytta och byta enstaka elektroner på ett kontrollerat sätt runt gruppen, en utmaning i sig. "
Tvådimensionella matriser kan styra fel
Kontrollfel som uppstår i enheterna är ett kapitel i sig. Datorerna vi använder idag ger många fel, men de korrigeras genom det som kallas upprepningskoden. I en vanlig dator, du kan ha information antingen i en 0 eller en 1. För att vara säker på att resultatet av en beräkning är korrekt, datorn upprepar beräkningen och om en transistor gör ett fel, det rättas med enkel majoritet. Om majoriteten av beräkningarna som utförs i andra transistorer pekar på 1 och inte 0, då väljs 1 som resultat. Detta är inte möjligt i en kvantdator eftersom du inte kan göra en exakt kopia av en qubit, så kvantfelkorrigering fungerar på ett annat sätt:Toppmoderna fysiska qubits har inte låg felfrekvens än, men om tillräckligt många av dem kombineras i 2-D-matrisen, de kan hålla varandra i schack, så att säga. Detta är en annan fördel med den nu realiserade 2-D-matrisen.
Nästa steg från denna milstolpe
Resultatet från Niels Bohr -institutet visar att det nu är möjligt att styra enstaka elektroner, och utföra experimentet i avsaknad av ett magnetfält. Så nästa steg blir att leta efter snurr - spinnsignaturer - i närvaro av ett magnetfält. Detta kommer att vara avgörande för att implementera enkla och två qubit -grindar mellan de enskilda qubitsna i arrayen. Teori har visat att en handfull enkla och två qubit portar, kallas en komplett uppsättning kvantportar, är tillräckligt för att möjliggöra universell kvantberäkning.