Med en lista över städer och avstånden mellan varje par städer, hur bestämmer du den kortaste rutten som besöker varje stad exakt en gång och återgår till startplatsen? Detta berömda problem kallas "resande säljare problem" och är ett exempel på ett kombinatoriskt optimeringsproblem. Att lösa dessa problem med konventionella datorer kan vara mycket tidskrävande, och speciella anordningar som kallas ”kvantglödgare” har skapats för detta ändamål.

Quantum annealers är utformade för att hitta det lägsta energitillståndet (eller marktillståndet) av det som kallas en Ising -modell. Sådana modeller är abstrakta representationer av ett kvantmekaniskt system som involverar interagerande snurr som också påverkas av yttre magnetfält. I slutet av 90 -talet, forskare fann att kombinatoriska optimeringsproblem kunde formuleras som Ising -modeller, som i sin tur fysiskt skulle kunna implementeras i kvantglödgare. För att få lösningen på ett kombinatoriskt optimeringsproblem, man måste helt enkelt observera marktillståndet som uppnås i dess associerade kvantglödgare efter en kort tid.

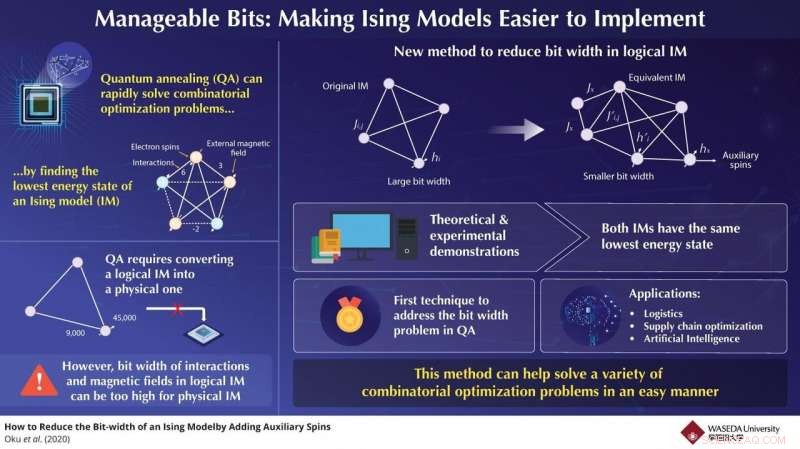
En av de största utmaningarna i denna process är omvandlingen av den logiska Ising -modellen till en fysiskt implementerbar Ising -modell som är lämplig för kvantglödgning. Ibland, de numeriska värdena för snurrinteraktionerna eller de yttre magnetfälten kräver ett antal bitar för att representera dem (bitbredd) för stora för ett fysiskt system. Detta begränsar kraftigt mångsidigheten och tillämpningen av kvantglödgare till verkliga problem. Lyckligtvis, i en ny studie publicerad i IEEE -transaktioner på datorer , forskare från Japan har hanterat denna fråga. Baserat enbart på matematisk teori, de utvecklade en metod genom vilken en given logisk Ising -modell kan omvandlas till en ekvivalent modell med önskad bitbredd för att få den att passa en önskad fysisk implementering.

Deras tillvägagångssätt består i att lägga till extra snurr till Ising -modellen för problematiska interaktioner eller magnetfält på ett sådant sätt att den transformerade modellens grundtillstånd (lösning) är densamma som den ursprungliga modellen samtidigt som den kräver en lägre bitbredd. Tekniken är relativt enkel och helt garanterad att producera en likvärdig Ising -modell med samma lösning som originalet. "Vår strategi är världens första att effektivt och teoretiskt ta itu med problemet med bitbreddreducering i spinninteraktioner och magnetfältkoefficienter i Ising-modeller, "säger professor Nozomu Togawa från Waseda University, Japan, som ledde studien.

Forskarna testade också sin metod i flera experiment, vilket ytterligare bekräftade dess giltighet. Professor Togawa har stora förhoppningar, och han avslutar med att säga, "Metoden som utvecklats i denna studie kommer att öka tillämpningen av kvantglödgare och göra dem mycket mer attraktiva för människor som inte bara hanterar fysiska Ising -modeller utan alla typer av kombinatoriska optimeringsproblem. Sådana problem är vanliga inom kryptografi, logistik, och artificiell intelligens, bland många andra områden. "