För att två former ska vara kongruenta måste var och en ha samma antal sidor och deras vinklar måste också vara desamma. Det enklaste sättet att avgöra om två former är kongruenta är att rotera en av formerna tills den är uppradad med den andra, eller helt enkelt stapla formen ovanpå varandra för att se om några ändar sticker ut. Om du inte kan flytta formerna fysiskt kan du använda formler för att bestämma om formerna är kongruenta.

Kongruenta cirklar

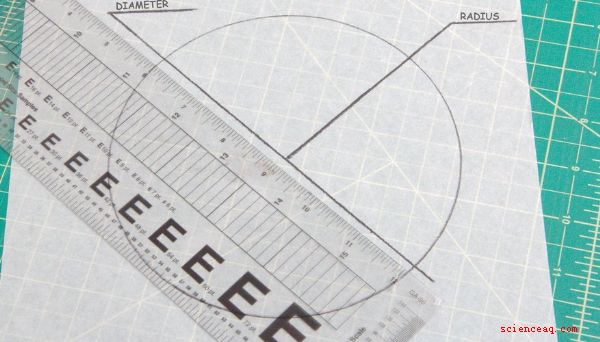
Alla cirklar har samma vinkel på 360 grader. Den enda faktorn för att bestämma kongruensen i två cirklar är att jämföra deras storlek. Diametern är en rak linje genom mitten av cirkeln från kant till kant, medan radien av en cirkel är längden från centrum till dess yttre kant. Mätning av någon av dessa i båda cirklarna kommer att visa sig om de är kongruenta.

Parallelogram

Ett parallellogram har två par parallella sidor, som torg och rektanglar. De motsatta sidorna eller vinklarna i ett parallellogram har samma mått, så det är nödvändigt att ta två vinklar eller sidmått på ett parallellogram, en från varje par sidor, för att jämföra kongruens med en annan form.

Trianglar

För att hitta trianglarnas kongruens måste du bestämma storleken på varje vinkel eller sida, eftersom alla tre kan vara olika. Det finns tre postulat som kan användas för att identifiera kongruenta trianglar. SSS-postulatet är när du mäter alla tre sidor i varje triangel. ASA-postulatet säger att om två vinklar och deras anslutande sida matchar den andra triangeln, då är de kongruenta. SAS-postulatet gör motsatsen, mäta två sidor och deras anslutningsvinkel för att jämföra med den andra triangeln.

Teorier för kongruenta trianglar

Två teoremer är användbara för att hitta kongruenta trianglar. AAS-teorin säger att om två vinklar och en sida som inte förbinder de två är lika med den för en annan triangel, så är de kongruenta. Hypotenus-Leg-steget gäller bara trianglar med en 90-graders eller "rätt" vinkel. Det här är när du mäter hypotenusen - sidan motsatt 90 graders vinkel - och en av de andra sidorna av triangeln, att jämföra med den andra formen.