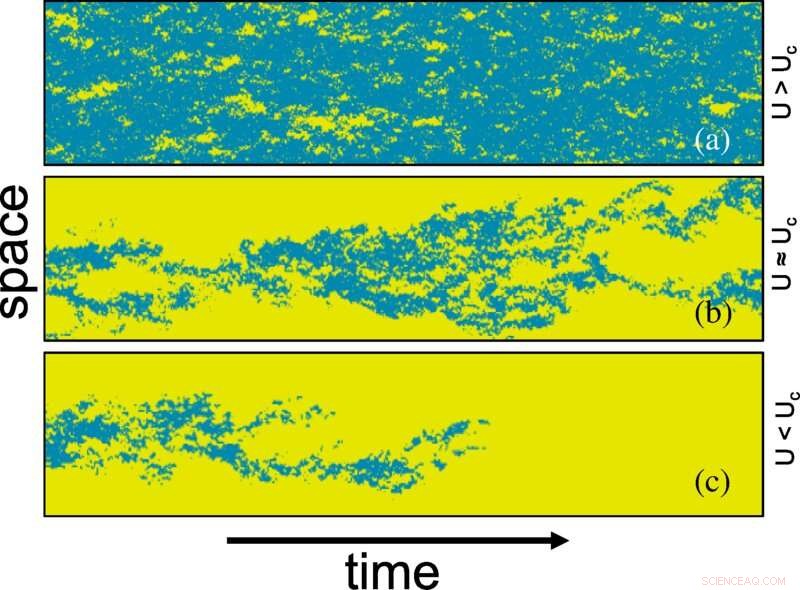
Rum-tid plot av laminär-turbulent övergång som en funktion av U (d.v.s. Reynolds nummer) genererad av PP-modellen i kvasi-1D Taylor-Couette-flöde. Turbulens (i blått) representeras av bytesdensiteten B, genererad av Monte Carlo-simulering på ett 2D-gitter med storleken 20×3000 (a) under den kritiska punkten U=0,0135, (b) vid den kritiska punkten U=0,01425, och (c) över den kritiska punkten U=0,0165. Gult representerar den laminära fasen som lokalt inte är upptagen av bytet. Bytesdensiteten binariseras beroende på om den är större än 0,065× maximal bytesdensitet. Kredit:Physical Review Letters (2022). DOI:10.1103/PhysRevLett.129.034501
Nämn ordet "turbulens" så kan du trolla fram bilder av ojämna flygningar, stormigt väder och hackiga havs- eller flodströmmar. För många är turbulens ett faktum i det dagliga livet, men det är också ett av de mest dåligt förstådda fysiska fenomenen. I synnerhet den punkt där en vätskas rörelse övergår från jämnt och förutsägbart flöde (känd som "laminärt") till slumpmässigt och oförutsägbart (känd som "turbulens") – den så kallade laminär-turbulenta övergången – fortsätter att förbrylla forskare sedan Osborne Reynolds studerade det först experimentellt i rör 1883.
Nu har ett team av forskare baserade vid University of Illinois Urbana-Champaign, University of California San Diego och Academia Sinica i Taiwan visat hur man redogör för de slumpmässiga mönstren och dynamiken för turbulens i rör under övergångsregimen. Deras arbete använder sig av nya idéer som har sitt ursprung i så olika områden som statistisk mekanik och ekologi och det bygger på de växande bevisen för att den laminära-turbulenta övergången har statistiska egenskaper som bäst kan tänkas i termer av teorin om fasövergångar som inte är jämviktsmässiga.
Teamet består av UIUC fysik doktorand Xueying Wang, Academia Sinica forskare Hong-Yan Shih och UIUC Swanlund begåvad professor emeritus i fysik och forskningsprofessor Nigel Goldenfeld. Goldenfeld är för närvarande kanslerernas framstående professor i fysik vid University of California San Diego.
Författarna publicerade sina resultat den 11 juli 2022 i tidskriften Physical Review Letters .
Puffar och sniglar är kännetecken för övergångsturbulens
Reynolds upptäckte att i rör sker den laminära-turbulenta övergången på ett ojämnt sätt när flödeshastigheten ökar. Klumpar av turbulent vätska, idag kända som "puffar", uppträder nära den laminära-turbulenta övergången och är åtskilda av områden med laminärt flöde. De exakta sätten på vilka puffarna uppträder och rör sig eller till och med delas i två beror på geometrin i det utrymme genom vilket en vätska strömmar. Dessa komplexa fenomen bidrar till turbulens välförtjänta rykte som ett av de sista utestående problemen inom klassisk fysik. Vid ännu högre hastigheter växer faktiskt turbulenta fläckar snarare än att bara flytta runt eller delas:dessa växande områden av turbulens kallas "sniglar".
För att bygga en tydligare bild av övergången till turbulens utvecklade forskarna en ny minimal modell för att förstå puffar och sniglar med hjälp av metoder importerade från teoretisk populationsbiologi. Forskarna fann att de kunde representera vätskans energiflöde nära den laminära-turbulenta övergången i termer av energiflödet som uppstår i ett rovdjur-byte ekosystem, där näringsämnen är energin i bakgrundsflödet, rovdjuret är en viss flödesstruktur som hämmar turbulens, och turbulens är bytet. Denna ekologiska modell rekapitulerar turbulent beteende i både rör och Taylor-Couette-flöde, en typ av rotationsflöde – ett mål som tidigare modeller inte lyckades uppnå.
Goldenfeld säger:"För sex år sedan gjordes ett genombrott med teoretiska och experimentella bevis som konvergerade på en beskrivning av turbulenta bloss som uppstår från laminärt flöde, i termer av fasövergångsteori. Men det arbetet lämnade frågan om vad som händer vid högre flöde öppen öppen. hastigheter bort från själva vändpunkten.
"Vårt nya arbete visar att samma konceptuella ramverk och metoder också gäller i snigelregimen och rekapitulerar i anmärkningsvärd detalj de experimentella fynden. Det är fantastiskt att se begrepp från fasövergångsteori och ekologi mötas i det helt andra problemet med vätskemekanik. "
Sniglar själva uppvisar intressanta beteenden och finns i två smaker, svaga sniglar och starka sniglar, som båda kännetecknas av minst en "front", en region som innehåller en gräns mellan laminära och turbulenta vätskor.
Huvudförfattaren Wang förklarar, "Framsidan av en snigel är som en väderfront. På ena sidan av fronten finns laminär vätska. På den andra sidan finns turbulens. Fronten är som en fasgräns, och den rör sig i rymden med ett stadigt hastighet. I rör får du både sniglar och bloss. Men svaga sniglar vid lägre vätskehastighet har bara en front uppströms, medan starka sniglar vid högre hastighet har fronter i både uppströms och nedströms riktningar. Dessa faktorer och rikedomen av övergångsfenomen gör att förstå övergångsturbulens riktigt svårt. Vårt arbete ger ett enhetligt ramverk som hanterar alla dessa regimer, olika flödesgeometrier och den inneboende slumpmässigheten."
Rovdjur-bytesmodeller och turbulens konvergerar
Forskarna kunde dra fördel av ett överraskande samband de hade funnit i tidigare arbete mellan populationsbiologi och övergångsturbulens.
Att modellera hur rovdjur interagerar med sina byten är ett populärt tema inom populationsbiologin. Grundidén är okomplicerad:rovdjur reproducerar och äter bytesdjur, vilket minskar deras befolkning; Byten förökar sig också, återställer deras antal och förser rovdjur med mat. Sedan upprepas cykeln. Enkelt uttryckt, rovdjur hämmar byten, medan byten förstärker rovdjur. Forskare kan härleda mycket information från dessa modeller, till exempel hur rovdjurs- och bytespopulationer varierar över tiden, samt hur lång tid det tar för var och en att dö ut orsakad av till exempel brist på mat eller överpredation.
I en tidigare studie visade Shih och Goldenfeld, som arbetade med före detta undergraduate Tsung-Lin Hsieh (nu postdoktor vid Princeton University), att det finns en analogi mellan rovdjur-bytesmodeller och turbulens som kan gjutas i matematiska termer. När vätska strömmar genom ett rör genereras två typer av vätskerörelser. Den första typen är ett virvelmönster som virvlar runt rörets axel, kallat "zonflöde". Den andra typen är turbulens längs röraxeln. Författarna fann att turbulens ackumuleras stadigt och aktiverar zonflöde, vilket därefter undertrycker turbulens. Med andra ord, zonflöde motsvarar rovdjur och turbulens motsvarar bytesdjur.
Forskarna fann att sannolikhetsfördelningen för livslängden för övergångsturbulens exakt matchade den för rovdjur och bytesdjur i ett ekosystem, ett fantastiskt samband med tanke på att populationsbiologi och vätskedynamik är till synes skilda områden.
Hong-Yan Shih comments, "This connection helps us understand the complex transitional behavior of turbulence from the point of view of phase transitions in statistical mechanics. Specifically, this discovery provides the key ingredients to construct an effective theory, which leads to the prediction that the laminar-turbulent transition in fluids is a non-equilibrium phase transition in the directed percolation universality class.
"Directed percolation can be thought of as the familiar process that happens when water drips through coffee grounds in a percolator. If the grounds are too tightly packed, water can't get through. On the other hand, if the grounds are too loosely packed, water can get through but the coffee is undrinkable. There's a critical point where the water just manages to get through and takes long enough so that the coffee tastes good.
"Mathematically, that phenomenon is exactly what happens in the transition to turbulence and the transition of a functioning ecosystem. The mathematics of phase transitions, founded in the Nobel Prize–winning work of K. Wilson, explains how this remarkable phenomenon arises."
This prior work, however, looked at the turbulence of a single puff. Real life isn't as simple, and real fluids near the laminar-turbulent transition contain multiple puffs that grow, die out, and interact in complex ways as the flow speed increases. The researchers needed to extend their model to capture more complicated dynamics beyond those of a single puff.
Extending the predator-prey model by incorporating nutrients
To capture the complex dynamics found in experiments beyond the critical point in the current study, the authors decided to take into account energy balance in pipe flow.
Wang explains, "Turbulence is a dissipative structure that needs constant energy input to be sustained, and that energy comes from the laminar flow. This fact was previously shown by exact computer simulations of the fluid equations, but did not allow us to understand in a predictive way the phenomena that would emerge."
The researchers realized that, just like zonal flow and turbulence require energy to persist, predators and prey need nutrients from their environment to survive.
"We wanted to make a minimal model of the full energy balance to extend the previous work and capture energy extraction of turbulence from laminar mean flow," Wang adds. "So we introduced another component into the 'ecosystem':nutrients, which represent the kinetic energy of the mean flow."
The researchers numerically simulated the extended predator-prey model on a two-dimensional lattice having a length much larger than its width. They watched what happens when nutrients—that is, laminar state energy, from the fluid dynamics perspective—flow into the ecosystem, are consumed by the turbulence, and are restored downstream of the turbulence.
The model maps several pathways for energy and population dynamics. The first pathway takes input energy from the energy budget to turbulent energy, like prey extracting nutrients from their environment. A second pathway takes turbulent energy to zonal flow energy, like predators eating prey.
Once they established these predator-prey-inspired pathways, they sat back and watched computer simulations based on the new model, wherein energy entered the pipe and passed through the pathways randomly. Out of the randomness emerged features of transitional turbulence such as puffs, slugs, and their associated fronts, reproducing results seen in experiments. The simulations showed that the appearance of puffs or slugs—and whether slugs are of the weak or strong type—is determined by the input energy (or equivalently, the speed) of the fluid flow.
The researchers then successfully reproduced all the transitional phenomena observed in pipe flow experiments and explained the underlying physics of puff splitting and growth. Specifically, they found that puff splitting and interaction is highly probabilistic. As the fluid speed increases, the probability of puff splitting also increases. The puff-slug transition is gradual, and it occurs when puffs split so frequently that they start to fill up the system densely.
Rotational flow and new questions for turbulence
In addition to pipe flow, the researchers also simulated a special type of rotational flow known as Taylor-Couette flow in which a fluid moves in the space between two concentric cylinders and the outer cylinder rotates relative to the inner one. Unlike pipe flow, where the energy enters from the high-pressure end of the pipe, Taylor-Couette flow is sustained by shear, the stress that occurs when two boundaries move parallel to one another. The new model easily incorporated this difference and reproduced the patterns of transitional turbulence seen in experiments, demonstrating the flexibility of the model.
"We showed that the rich and complicated dynamical features in transitional pipe flow can be understood with a simple three-level stochastic predator-prey model based on energy balance in pipe flow," says Wang. "Our model also works for quasi-one-dimensional Taylor-Couette flow. Since energy balance generally holds in fluid systems, we expect our model to be applicable to systems with more complicated geometries as well."
Having described turbulence broadly by implementing their model in two different geometries, the team is already looking to answer new questions.
Goldenfeld says, "The next challenge is to see if and how our probabilistic model can be extended to two- or three-dimensional flows. This problem has been intensely studied for well over twenty years, with new experimental data starting to appear."
For his part, Goldenfeld is pleased to see diverse techniques converge to solve problems in complementary ways, a beautiful demonstration of how different fields of science can inform each other.
Goldenfeld summarizes, "Our results show how stochastic dynamics, pattern formation, phase transitions, and modeling concepts from diverse fields such as ecology can bring new tools, predictions, and insights into a problem previously considered within the more narrow disciplinary focus of fluid dynamics. It is exciting to see how successful minimal modeling is at capturing complex physical phenomena in a quantitative way." + Utforska vidare