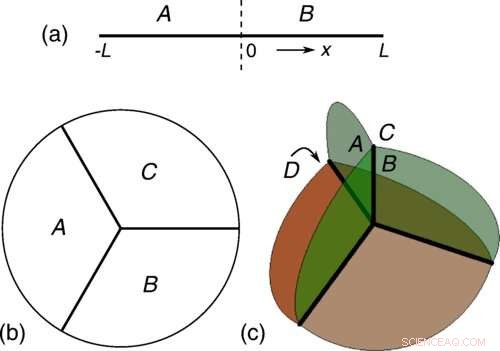
Den D-dimensionella Fermi-gasen för (a) D=1, (b) D=2 och (c) D=3 är uppdelad i D+1-regioner som möts i en enda punkt, med alla k regioner som delar en platt gräns av dimension D + 1 - k. Här studerar vi ett intrasslingsmått, känt som den ömsesidiga informationen, som fångar de inneboende korrelationerna mellan alla D + 1-regioner. Den ömsesidiga informationen är topologisk genom att den uppvisar en ledande logaritmisk divergens som är proportionell mot Euler-karakteristiken χF av Fermihavet. Kredit:Pok Man Tam et al, Physical Review X (2022). DOI:10.1103/PhysRevX.12.031022
Topologi och intrassling är två kraftfulla principer för att karakterisera strukturen hos komplexa kvanttillstånd. I en ny artikel i tidskriften Physical Review X , etablerar forskare från University of Pennsylvania en relation mellan de två.
"Vårt arbete knyter samman två stora idéer", säger Charles Kane, Christopher H. Browne framstående professor i fysik vid Penns School of Arts &Sciences. "Det är en begreppsmässig länk mellan topologi, som är ett sätt att karakterisera de universella egenskaperna som kvanttillstånd har, och intrassling, vilket är ett sätt på vilket kvanttillstånd kan uppvisa icke-lokala korrelationer, där något som händer i en punkt i rymden är korrelerade med något som händer i en annan del av rymden. Vad vi har hittat är en situation där dessa begrepp är tätt sammanflätade."
Fröet till att utforska detta samband kom under de långa timmar som Kane tillbringade på sitt hemmakontor under pandemin och funderade över nya idéer. En tankegång fick honom att föreställa sig den klassiska läroboksbilden av Fermi-ytan av koppar, som representerar metallens potentiella elektronenergier. Det är en bild som alla fysikstudenter ser, och en som Kane var mycket bekant med.
"Naturligtvis lärde jag mig om den bilden redan på 1980-talet men hade aldrig tänkt på det som att beskriva en topologisk yta," säger Kane.
Ett klassiskt sätt att tänka om topologiska ytor, säger Kane, är att överväga skillnaden mellan en munk och en sfär. Vad är skillnaden? Ett enda hål. Topologi tar hänsyn till dessa generaliserbara egenskaper hos en yta, som inte förändras av deformation. Enligt denna princip skulle en kaffekopp och en munk ha samma topologiska egenskap.
Om man betraktar Fermi-ytan av koppar som ett topologiskt objekt, är det associerade antalet hål som den har fyra, en figur som också kallas ett släkte. När Kane började tänka på Fermi-ytan på det här sättet, undrade han om ett förhållande kunde existera mellan släktet och kvantförveckling.
För att ytterligare undersöka den potentiella kopplingen involverade Kane sin doktorand Pok Man Tam och Martin Claassen, en biträdande professor i fysik vid Penn som har fokuserat på kvantintrassling i sitt arbete. Tillsammans härledde de ett matematiskt förhållande mellan släktet på Fermi-ytan och ett mått på kvantförveckling som kallas den ömsesidiga informationen. Den ömsesidiga informationen kännetecknar de korrelationer som kan uppstå i olika delar av rymden som möts vid en enda punkt. Ett nummer känt som Euler-egenskapen, som är nära besläktat med släktet, gav den exakta kopplingen mellan de två.
Forskarna fastställde att förhållandet mellan topologi och intrassling som hålls i ett enkelt metallsystem, med elektroner som rör sig oberoende av varandra, utökade sedan sin analys för att visa att kopplingen också var närvarande även när elektroner interagerade med större komplexitet.
Och medan det teoretiska arbetet gjordes på metaller, tror Kane att det kommer att sträcka sig till andra material också, till exempel de som involverar mycket starka interaktioner mellan elektroner.
"Vad detta kan tillåta oss att göra är att ta fram nya sätt att tänka på faser av materia som vi inte förstår så väl och som inte har så många verktyg för att utforska," säger Kane. "Människor försöker ta reda på hur man kan utnyttja kvantmekaniken för att dra fördel av kvantinformation. För att kunna göra det måste du förstå hur kvantmekaniken visar sig när du har många frihetsgrader. Det är ett mycket svårt problem, och det här arbetet driver oss i den riktningen."
In follow-up work, Kane and colleagues hope to design experiments that continue to explore the newfound link, perhaps devising a new technique to measure the topological genus and a way to probe the structure of quantum entanglement. + Utforska vidare