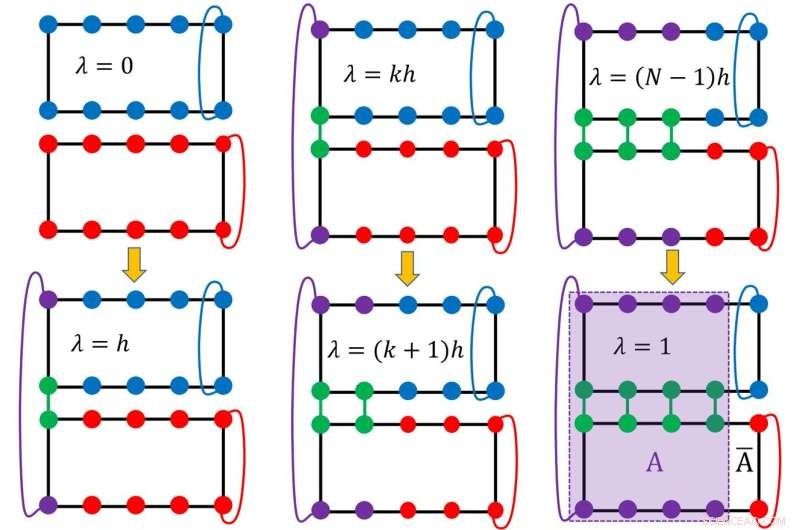
Figur 1. Den schematiska kurvan för det numeriska experimentet. Kredit:University of Hong Kong
Via storskaliga simuleringar på superdatorer upptäckte ett forskarlag från Institutionen för fysik, University of Hong Kong (HKU), tydliga bevis för att karakterisera en mycket intrasslad kvantmateriafas - kvantspinnvätskan (QSL), en fas av materia som förblir oordnad även vid mycket låga temperaturer. Denna forskning har nyligen publicerats i npj Quantum Materials .
QSL föreslogs 1973 av P. W. Anderson, nobelpristagaren för fysik 1977. De har potential att användas i topologisk kvantberäkning och att hjälpa till att förstå mekanismerna hos högtemperatursupraledare som avsevärt kan minska energikostnaderna under eltransporter på grund av frånvaro av elektriskt motstånd.
QSL kallas en vätska på grund av sin brist på konventionell ordning. QSLs har en topologisk ordning som härrör från långväga och stark kvantintrassling. Detekteringen av denna topologiska ordning är en tuff uppgift på grund av bristen på material som perfekt kan uppnå de många modellsystem som forskare föreslår för att hitta en topologisk ordning av QSL och bevisa dess existens. Det har alltså inte funnits bestämt accepterade konkreta bevis som visar att QSL finns i naturen.
Jiarui Zhao, Dr Bin-Bin Chen, Dr Zheng Yan och Dr Zi Yang Meng från HKU Institutionen för fysik undersökte framgångsrikt denna topologiska ordning i en fas av Kagome gitterkvantspinmodell, som är en tvådimensionell gittermodell med inneboende kvantintrassling och föreslagna av forskare som har Z2 (en cyklisk grupp av ordning 2) topologisk ordning, via ett noggrant utformat numeriskt experiment på superdatorer. Deras entydiga resultat av topologisk intrasslingsentropi tyder starkt på existensen av QSLs i kvantmodeller med hög intrassling ur ett numeriskt perspektiv.
"Vårt arbete drar fördel av den överlägsna beräkningskraften hos moderna superdatorer, och vi använder dem för att simulera en mycket komplicerad modell som tros ha topologisk ordning. Med våra fynd är fysiker mer övertygade om att QSL:er borde finnas i naturen", säger Jiarui Zhao, den första författaren till tidskriften och en Ph.D. student vid institutionen för fysik.
"Numeriska simuleringar har varit en viktig trend inom vetenskaplig forskning av kvantmaterial. Våra algoritmer och beräkningar skulle kunna hitta mer intressant och ny kvantmateria och sådana ansträngningar kommer säkerligen att bidra till utvecklingen av både praktisk kvantteknologi och det nya paradigmet inom grundforskning." sa Dr Zi Yang Meng, docent vid institutionen för fysik.
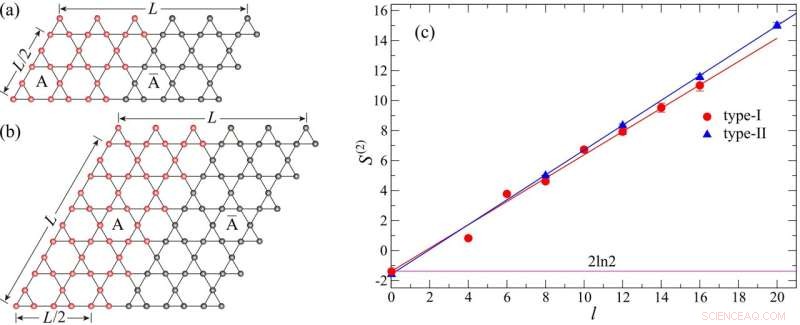
Figur 2. Gittertyperna för Kagome kvantspinnmodell och motsvarande resultat av topologisk entropi. Kredit:University of Hong Kong
Undersökningen
Teamet designade ett numeriskt experiment på Kagome-spinmodellen (Kagome är en tvådimensionell gitterstruktur som visar ett liknande mönster som ett traditionellt japanskt vävt bambumönster i form av hexagonalt gallerverk) i den föreslagna QSL-fasen, och den schematiska plotten av experimentet illustreras i figur 1. Entanglement-entropin (S) för ett system kan erhållas genom att mäta förändringen av modellens fria energi under en noggrant utformad icke-jämviktsprocess. Den topologiska entropin (γ), som kännetecknar långdistans topologisk ordning, kan extraheras genom att subtrahera kortdistansbidraget, som är proportionellt mot längden på intrasslingsgränsen (l) från den totala intrasslingsentropin(S), genom att anpassa data för intrasslingsentropi av olika sammantrasslingsgränslängd till en rät linje (S=al-γ).
Som visas i figur 2 genomförde teamet experimentet på två typer av galler med olika förhållanden mellan längd och bredd för att säkerställa resultatens tillförlitlighet. Forskarna använde en rät linje för att anpassa förhållandet mellan intrasslingsentropin med längden på intrasslingsgränsen så att den topologiska entropin skulle vara lika med skärningen av den räta linjen. Resultaten ger värdet på topologisk entropi till 1,4(2), vilket är i överensstämmelse med det förutsagda värdet av topologisk entropi för en Z2 kvantspinnvätska, som är 2ln (2). Fynden bekräftar förekomsten av QSLs ur ett numeriskt perspektiv. + Utforska vidare