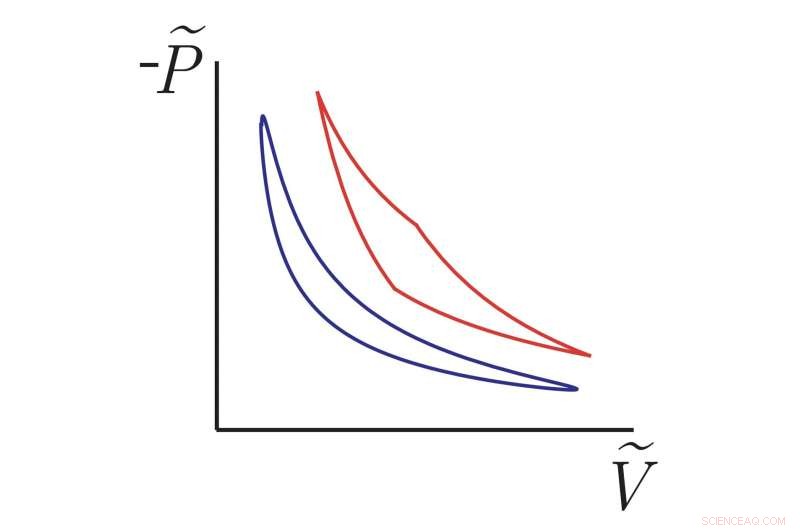
Nyupptäckta termodynamiska cykler (jämn blå kurva) närmar sig en ny geometrisk gräns för effektivitet och överträffar andra icke-jämviktsmotorer som Carnot-cykeln (röd kurva) som fungerar i ändlig tid. De vertikala och horisontella axlarna representerar analoger av (negativt) tryck och volym för en mikroskopisk motor som består av en partikel fäst vid en fjäder som drabbas av termiska fluktuationer från dess omgivning. Dessa är teoretiska kurvor baserade på våra matematiska resultat, men experimentalister har nyligen utarbetat metoder för att mäta effektiviteten hos dessa typer av system så att våra resultat kan testas. Kredit:Frim &DeWeese.
Stokastisk termodynamik är ett framväxande område inom fysiken som syftar till att bättre förstå och tolka termodynamiska begrepp bort från jämvikt. Under de senaste åren har fynd inom dessa områden revolutionerat den allmänna förståelsen av olika termodynamiska processer som fungerar i begränsad tid.
Adam Frim och Mike DeWeese, två forskare vid University of California, Berkeley (UC Berkeley), har nyligen genomfört en teoretisk studie som utforskar hela utrymmet av termodynamiska cykler med en kontinuerligt föränderlig badtemperatur. Deras resultat, presenterade i en artikel publicerad i Physical Review Letters , erhölls med användning av geometriska metoder. Termodynamisk geometri är ett tillvägagångssätt för att förstå responsen hos termodynamiska system genom att studera det geometriska kontrollrummet.
"Till exempel, för en gas i en kolv, kan en koordinat i detta kontrollutrymme motsvara den experimentellt kontrollerade volymen av gasen och en annan till temperaturen," sa DeWeese till Phys.org. "Om en experimentalist skulle vrida på dessa rattar, ritar det ut en bana i detta termodynamiska utrymme. Vad termodynamisk geometri gör är att tilldela varje kurva en 'termodynamisk längd' som motsvarar den minsta möjliga förbrukade energin för en given bana."
Termodynamisk geometri tillåter forskare att undersöka intressanta forskningsfrågor, som det optimala sättet att manipulera ett givet nanoskopiskt system, radera lite information eller bygga en klassisk eller kvantvärmemotor.
"Vårt huvudmål i det här dokumentet var att ta reda på det mest effektiva sättet att köra en mikroskopisk motor så att den producerar det mest användbara arbetet för den mängd bränsle den förbrukar," sa DeWeese till Phys.org. "Medan de flesta tidigare termodynamiska geometristudier fokuserade på att optimera styrningen av ett system med givna initiala och slutliga inställningar, var vi intresserade av att konstruera optimala slutna kurvor som skulle kunna fungera som högeffektiva värmemotorer."
De viktigaste "reglerna" för att förstå hur man effektivt kör stora motorer, som de inuti bilar, när de körs långsamt, beskrevs först för över ett sekel sedan, när termodynamikens lagar först formulerades. I sin uppsats utökade Frim och DeWeese dessa teorier så att de också kunde tillämpas på mikroskopiska motorer som fungerar i begränsad tid. Till skillnad från långsamt arbetande stora motorer är dessa motorer inte i termisk jämvikt med omvärlden och påverkas starkt av termiska fluktuationer i den omgivande miljön.
"I alla termodynamikkurser på grundnivå lär vi oss att om du plottar tryck vs. volym av en gas i en cylinder och överväger varje sluten cykel som återgår till samma punkt på grafen, ger området som finns i kurvan dig mängden användbar arbete du får från en cykel av denna värmemotor," sa DeWeese. "Detta förutsätter att du rör dig mycket långsamt runt cykeln, så att gasen i cylindern alltid förblir nära jämvikt med omvärlden. Det finns en analogi till detta P-V-diagram för mikroskopiska motorer, till exempel en liten partikel fäst vid en fjäder drabbas av termiska fluktuationer från sin omgivning."
När de ritade cykler på analogen av ett P-V-diagram för en mikroskopisk motor, fann Frim och DeWeese att en speciell funktion av området inuti den stängda kurvan fortfarande kunde betraktas som mängden användbart arbete som en cykel av motorn tillhandahåller. . Dessutom visade sig längden på den stängda kurvan vara relaterad till mängden "nyttigt arbete" som har gått förlorat till förlust (d.v.s. värma upp miljön utan att gå mot motorns drift).
"Vårt resultat är relativt enkelt konceptuellt," förklarade DeWeese. "I termodynamisk geometri är längd ungefär som förlust. Så, vi tänkte då:om du tar en cykel (en sluten slinga) med någon omkrets som har en fast längd, vad representerar området inuti denna slinga? Som det visar sig är det liknar cykelns arbetseffekt, så egentligen borde optimala cykler ha låg förlust och hög effekt, dvs. en liten längd och en stor yta."
Genom att utnyttja klassiska geometriska resultat kunde forskarna sedan identifiera optimala protokoll som satte en gräns för effektiviteten hos alla slutna cykler. Deras resultat kan avsevärt bidra till design och utveckling av effektiva mikroskopiska värmemotorer. Bindningen på effektiviteten hos irreversibla termodynamiska cykler som fastställts av detta team av forskare är generell, så dess implikationer kan sträcka sig långt bortom de specifika mikroskopiska motorer som tas upp i deras artikel.
"Ett av våra långsiktiga mål är att utveckla teorin som behövs för ingenjörer att designa och bygga mycket små och effektiva motorer," sa DeWeese. "Detta kan visa sig vara ett viktigt område inom nanoteknik. Vi är också starkt motiverade att förstå strukturen och funktionen hos de molekylära motorerna och andra typer av molekylära 'maskiner' som vi ser i cellerna hos alla varelser och växter."
I sitt arbete antar De Weese och Frim att naturlig evolution kan ha valt för effektiva molekylära maskiner. Om så vore fallet skulle reglerna de upptäckt vara ett första steg mot att kunna förutsäga strukturen och funktionen hos molekylära maskiner som är allestädes närvarande i biologin.
"Isoperimetriska ojämlikheter (det vill säga samspelet mellan längder och ytor av stängda kurvor) i geometriska tillvägagångssätt för fysik kan ha otaliga konsekvenser framöver," tillade DeWeese. "Vår matematiska gräns är mer realistisk än tidigare resultat som antog att motorn var mycket nära termisk jämvikt med miljön (eller värmebad) hela tiden, men vi antar fortfarande att systemet körs långsamt (dvs kontrollparametrarna) förändras långsamt). Vi är nu intresserade av att utöka våra resultat bortom denna regim till att omfatta system längre från jämvikt." + Utforska vidare
© 2022 Science X Network