En ny studie av forskare från Japan utforskar spridningen av kvantinformation inom interagerande bosonsystem som Bose-Einstein-kondensat (BEC), vilket avslöjar potentialen för accelererad överföring till skillnad från tidigare trott.
Kvantsystem för många kroppar, som interagerande bosonsystem, är fundamentalt viktiga eftersom de hittar tillämpningar inom olika grenar av fysiken. Spridningen av information i kvantsystem med många kroppar styrs av Lieb-Robinson-bunden. Detta kvantifierar hur snabbt information eller förändringar sprider sig genom ett kvantsystem.
När du gör en förändring i en del av systemet, beskriver Lieb-Robinson bound den hastighet med vilken denna förändring påverkar andra delar av systemet. Rent praktiskt betyder det att effekten av din första förändring kommer att spridas utåt från dess ursprungspunkt, vilket påverkar närliggande regioner i systemet.
Men Lieb-Robinson på väg mot interagerande bosonsystem har länge varit en utmaning.
Forskarna, ledda av Dr. Tomotaka Kuwahara, RIKEN Hakubi Team Leader vid RIKEN Center for Quantum Computing, tar sig an denna utmaning i sin nya Nature Communications studera.
Dr. Kuwahara förklarade vikten av deras arbete för Phys.org och betonade vikten av att förstå kvantsystem som innehåller fundamentala partiklar som bosoner och fermioner.
"Bosonsystemen har i princip ingen energigräns, vilket gjorde Lieb-Robinson bunden i bosoniska system avsevärt utmanande", sa han.
Som tidigare nämnts ger Lieb-Robinson-bindningen en kvantitativ gräns för hur snabbt korrelationer eller influenser kan spridas mellan rumsligt åtskilda regioner i ett kvantsystem.
Vad detta betyder är att spridningen inte kan ske direkt överallt utan istället begränsas till en effektiv ljuskon. Inspirerad av Einsteins relativitetsteori representerar ljuskonen alla punkter i rum och tid som en ljussignal som sänds ut från en händelse kan nå. Detta skapar en dubbel kon:en för det förflutna och en för framtiden.
Detsamma gäller informationsspridning i kvantmångkroppssystem, d.v.s. system med fler än två kvantpartiklar.
"Lib-Robinson bound sätter en universell hastighetsgräns för hur snabbt information kan färdas i dessa system", förklarade Dr. Kuwahara.
Enligt Lieb-Robinson-bunden är spridningen av information begränsad och avtar exponentiellt med avstånd eller tid. Detaljerna för förfallet beror på det individuella systemet och de interaktioner som kan uppstå inom systemet.
Formulerad av Elliott Lieb och Derek Robinson 1972, är Lieb-Robinson-bindningen endast tillämplig för icke-relativistiska system, vilket vill säga att informationen färdas med hastigheter som är mycket lägre än ljusets hastighet.
Interagerande bosonsystem består av många bosoner (som fotoner). Även om dessa system är vanliga, erbjuder de många utmaningar, såsom långväga interaktioner mellan bosoner och ogränsad energi, vilket gör det svårt att utveckla simuleringar och teoretiska modeller.
Men sedan upptäckten av BEC har modeller som Bose-Hubbard-modellen utvecklats för att studera bosoniska system. Bose-Hubbard-modellen är ett teoretiskt ramverk som används för att förstå hur bosoner beter sig när de är begränsade till en gitterstruktur, som atomer i en kristall.
Denna modell tar hänsyn till två huvudfaktorer. Först är hoppningen av bosoner från en gitterplats till en annan, representerad av hoppningsparametern. Den andra är interaktionsparametern på plats, som representerar de frånstötande krafterna mellan bosoner när de upptar samma plats. Denna interaktionsenergi ökar när fler bosoner upptar samma plats.
Dessa faktorer inkluderar interaktionen mellan bosonerna, vilket är anledningen till att forskarna valde Bose-Hubbard-modellen för att undersöka Lieb-Robinsons gränser i interagerande bosonsystem.
Forskarna valde att studera Lieb-Robinson bunden till ett D-dimensionellt gitter (samverkande bosonsystem) styrt av Bose-Hubbard-modellen. De hittade tre resultat för detta system.
Detta resultat adresserar interaktionen mellan bosoner inom gittret. Forskarna fann att hastigheten för bosontransport är begränsad, även i system med långväga interaktioner. Denna hastighet, även om den är begränsad, växer som mest logaritmiskt med tiden, vilket är relativt långsamt.
Detta fynd ger avgörande insikter om dynamiken i bosonsystem, vilket sätter en övre gräns för dess hastighet.
Detta resultat fokuserar på spridningen av operatörer av systemet över tiden. Operatörer är i grunden variabler i systemet, som momentum. När dessa operatörer fortplantar sig avviker de från den ideala utvecklingen, vilket leder till ackumulering av fel.
Denna felspridning avgör hur snabbt information kan spridas i systemet. Till exempel, om felet är stort, indikerar det att informationsspridningen är långsammare eller mer begränsad, eftersom approximationen avviker avsevärt från den ideala utvecklingen av systemet.
På samma sätt, om felet är litet, så är informationsspridningen snabb. Detta överensstämmer med Lieb-Robinson-gränsen, vilket indikerar närvaron av en övre gräns för felutbredning.
Trots närvaron av en övre gräns för felutbredning, inducerar interaktioner mellan bosoner klustring i specifika regioner. Dessa regioner, som kännetecknas av högre bosonkoncentrationer, underlättar accelererad informationsutbredning längs vissa gittervägar eller riktningar.
Detta fenomen överensstämmer med Lieb-Robinson bundna. Denna acceleration är dock begränsad och har en polynomtillväxt beroende på systemets dimensionalitet.
Detta resultat presenterar ett sätt att simulera dessa system med hjälp av elementära kvantportar (som CNOT). Forskarna ger en övre gräns för antalet elementära kvantportar som krävs för att effektivt simulera tidsutvecklingen för interagerande bosonsystem.
Fermioniska system visar en begränsad hastighetsgräns för hur snabbt information kan spridas. Innan detta arbete antog forskare detsamma för bosoniska system, vilket är osant.
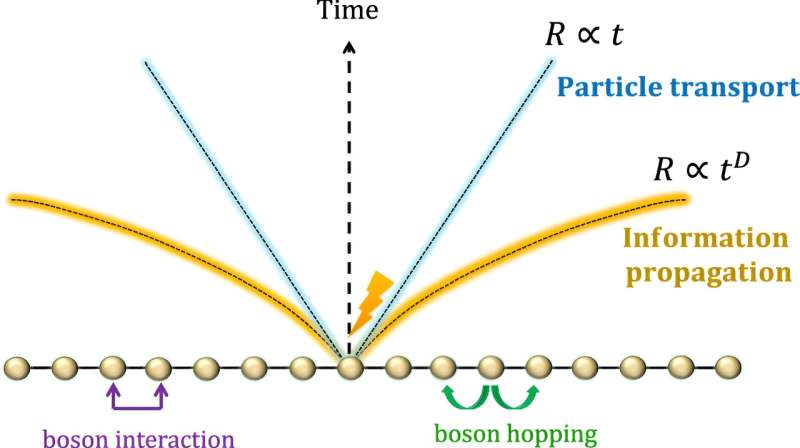
"Ljuskonen sprider sig mycket snabbare och är icke-linjär, det vill säga snabbar upp med tiden. Närmare bestämt, om du tittar på ett tredimensionellt utrymme, växer avståndet "information" kan resa med tidens kvadrat. Så i denna mening kan bosoner skicka information mycket snabbare än fermioner kan, särskilt när tiden går", förklarade Dr. Kuwahara.
Detta beror på antalet bosoner som kan ockupera samma stat samtidigt. I grund och botten, ju fler bosoner som går med, desto snabbare kan information spridas.
"Men eftersom bosoner bara kan röra sig med en ändlig hastighet, tar det lite tid för många av dem att komma samman, vilket leder till en begränsad hastighet för informationsutbredning. Med tiden, när fler bosoner samarbetar, den hastighet med vilken de kan skicka information går upp", sa Dr. Kuwahara.
Detta arbete öppnar ett nytt fönster för att utforska interagerande bosonsystem för informationsspridning.
"Jag räknar med att algoritmen kommer att användas för att simulera den kondenserade materiens fysik, vilket kan leda till upptäckten av nya kvantfaser. Den borde också visa sig användbar för att simulera kvanttermalisering, hjälpa till att ta itu med den grundläggande frågan om hur slutna kvantsystem sätter sig i en steady state över tid", avslutade Dr. Kuwahara.
Mer information: Tomotaka Kuwahara et al, Effektiv ljuskon och digital kvantsimulering av interagerande bosoner, Nature Communications (2024). DOI:10.1038/s41467-024-46501-7.
Journalinformation: Nature Communications
© 2024 Science X Network