Föreställ dig en värld där komplexa beräkningar som för närvarande tar månader för våra bästa superdatorer att knäcka kan utföras på några minuter. Quantum computing revolutionerar vår digitala värld. I en forskningsartikel publicerad i Intelligent Computing , avslöjade forskare en automatiserad protokolldesignstrategi som kan låsa upp beräkningskraften hos kvantenheter snabbare än vi föreställt oss.
Kvantberäkningsfördelar representerar en kritisk milstolpe i utvecklingen av kvantteknologier. Det betyder kvantdatorers förmåga att överträffa klassiska superdatorer i vissa uppgifter. För att uppnå kvantberäkningsfördelar krävs specialdesignade protokoll. Slumpmässig kretssampling, till exempel, har visat lovande resultat i de senaste experimenten.
En fråga som måste beaktas vid försök att använda slumpmässig kretssampling är att strukturen hos en slumpmässig kvantkrets måste utformas noggrant för att öka gapet mellan kvantberäkning och klassisk simulering. För att möta utmaningen utvecklade forskarna He-Liang Huang, Youwei Zhao och Chu Guo en automatiserad protokolldesignstrategi för att bestämma den optimala slumpmässiga kvantkretsen i experiment med kvantberäkningsfördelar.
Kvantprocessorarkitekturen som används för slumpmässiga kretssamplingsexperiment använder 2-qubit-grindmönster. 2-qubit-grinden realiserar interaktionen mellan de två kvantbitarna genom att verka på tillstånden för de två kvantbitarna, och därigenom konstruera en kvantkrets och realisera kvantberäkning.
Det är nödvändigt att maximera den klassiska simuleringskostnaden för att säkerställa att den överlägsna prestandan hos kvantberäkningar utnyttjas fullt ut när beräkningar utförs. Att bestämma den optimala slumpmässiga kvantkretsdesignen för att maximera kostnaden för klassisk simulering är dock inte lätt.
För att hitta den optimala slumpmässiga kvantkretsen måste man först uttömma alla möjliga mönster, sedan uppskatta den klassiska simuleringskostnaden för var och en av dem och välja den med högst kostnad. Den klassiska simuleringskostnaden är starkt beroende av vilken algoritm som används, men den traditionella algoritmen har för närvarande begränsningen att uppskattningstiden är för lång.
Den nya metoden som föreslagits av författarna använder Schrödinger-Feynman-algoritmen. Denna algoritm delar upp systemet i två delsystem och representerar deras kvanttillstånd som tillståndsvektorer. Kostnaden för algoritmen bestäms av den intrassling som genereras mellan de två delsystemen. Att utvärdera komplexiteten med denna algoritm kräver mycket mindre tid, och fördelarna blir mer uppenbara när den slumpmässiga kvantkretsstorleken ökar.
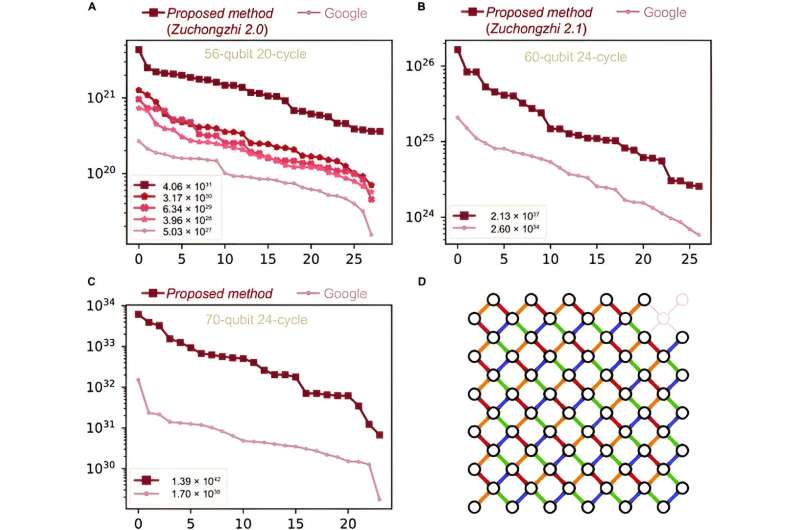
Författarna bevisade experimentellt effektiviteten hos den slumpmässiga kvantkretsen som erhölls med den föreslagna metoden jämfört med andra algoritmer. Fem slumpmässiga kvantkretsar genererades i Zuchongzhi 2.0 kvantprocessor, var och en med olika Schrödinger-Feynman-algoritmkomplexitet. Experimentella resultat visar att kretsar med högre komplexitet också har högre kostnader.
Rivaliteten mellan klassisk och kvantberäkning förväntas avslutas inom ett decennium. Detta nya tillvägagångssätt maximerar beräkningskraften hos kvantberäkningar utan att ställa nya krav på kvanthårdvaran. Dessutom kan den främsta anledningen till att detta nya tillvägagångssätt kan erhålla slumpmässiga kvantkretsar med högre klassiska simuleringskostnader vara den snabbare tillväxten av kvanttrassling.
I framtiden kan förståelsen av detta fenomen och dess underliggande fysik hjälpa forskare att utforska praktiska tillämpningar med hjälp av kvantfördelarexperiment.
Mer information: He-Liang Huang et al, Hur man designar en klassiskt svår slumpmässig kvantkrets för kvantberäkningsfördelarexperiment, Intelligent beräkning (2024). DOI:10.34133/icomputing.0079
Tillhandahålls av Intelligent Computing