Ekvationen för en linje är av formen y = mx + b, där m representerar lutningen och b representerar linjans korsning med y-axeln. Den här artikeln visar med exempel hur vi kan skriva en ekvation för linjen som har en given sluttning och passerar genom en given punkt.

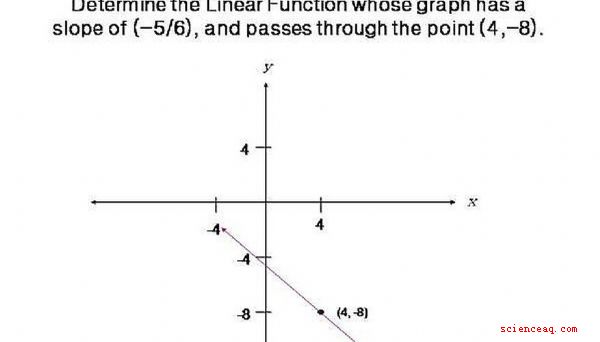
Vi hittar den linjära funktionen, vars graf har en lutning på (-5 /6) och passerar genom punkten (4, -8). Vänligen klicka på bilden för att se diagrammet.

För att hitta Linjärfunktionen använder vi formeln Slope-Intercept, vilket är y = mx + b. M är linjens lutning och b är y-avlyssningen. Vi har redan linjens lutning, (-5/6), så vi kommer att ersätta m med lutningen. y = (- 5/6) x + b. Klicka på bilden för att få en bättre förståelse.

Nu kan vi ersätta x och y med värdena från den punkt som linjen går igenom, (4, -8). När vi ersätter x med 4 och y med -8 får vi -8 = (- 5/6) (4) + b. Genom att förenkla uttrycket får vi -8 = (- 5/3) (2) + b. När vi multiplicerar (-5/3) med 2 får vi (-10/3). -8 = (- 10/3) + b. Vi lägger till (10/3) på båda sidor av ekvationen, och genom att kombinera liknande termer får vi: -8+ (10/3) = b. För att lägga till -8 och (10/3) måste vi ge -8 en nämnare av 3. För att göra detta, vi mulitply -8 av (3/3), vilket är lika med -24/3. Vi har nu (-24/3) + (10/3) = b, vilket är lika med (-14/3) = b. Klicka på bilden för att få en bättre förståelse.

Nu när vi har värdet för b kan vi skriva linjärfunktionen. När vi ersätter m med (-5/6) och b med (-14/3) får vi: y = (- 5/6) x + (- 14/3), vilket är lika med y = (- 5/6 ) x- (14/3). Vänligen klicka på bilden för bättre förståelse.