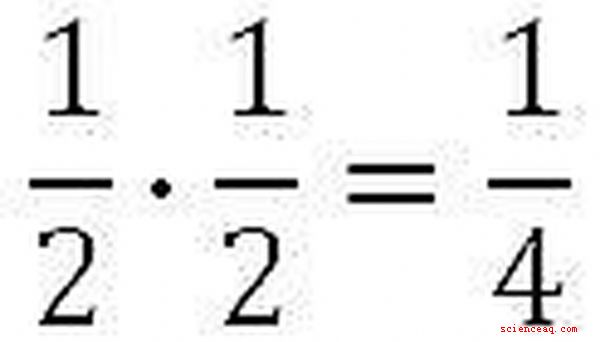
Detta är artikel 1 i en serie fristående artiklar om grundläggande sannolikhet. Ett vanligt ämne i introduktionssannolikheten är att lösa problem med myntflipar. I den här artikeln visas stegen för att lösa de vanligaste typerna av grundläggande frågor om detta ämne.
Först noterar du att problemet sannolikt kommer att referera till ett "rättvist" mynt. Allt detta betyder att vi inte hanterar ett "trick" -mynt, som en som har vägats att landa på en viss sida oftare än den skulle ha.
För det andra, problem som det här aldrig involvera någon typ av silliness, som mynt landning på dess kant. Ibland försöker eleverna att lobbyn för att få en fråga som anses vara ogiltig på grund av något försenat scenario. Ta inte med någonting i ekvationen som vindmotstånd, eller om Lincolns huvud väger mer än hans svans eller något sådant. Vi har att göra med 50/50 här. Lärarna blir verkligen upprörda över vad som helst annat.
Med allt sagt är här en mycket vanlig fråga: "En rättvis mynt landar på huvuden fem gånger i rad. Vilka är riskerna att det kommer att landa på huvuden på nästa flip? " Svaret på frågan är helt enkelt 1/2 eller 50% eller 0,5. Nu räcker det. Alla andra svar är fel.
Sluta tänka på vad det än är som du tänker på just nu. Varje flip av ett mynt är helt oberoende. Myntet har inget minne. Myntet blir inte "uttråkat" av ett givet resultat och önskar byta till något annat, och det har inte heller någon önskan att fortsätta ett visst resultat eftersom det är "på rulle". Jo fler gånger du snubblar ett mynt desto närmare kommer du att få 50% av flipparna som huvud, men det har fortfarande inget att göra med någon enskild flip. Dessa idéer består av det som kallas Gambler's Fallacy. Se Resurs sektionen för mer.
Här är en annan vanlig fråga: "Ett rättvist mynt vändes två gånger. Vilka är riskerna att det kommer att landa på huvuden på båda fliparna?" Vad vi har att göra med här är två oberoende händelser, med ett "och" villkor. Enkelt sagt, varje flip på myntet har inget att göra med någon annan flip. Dessutom handlar det om en situation där vi behöver en sak att hända, "och" en annan sak. "
I situationer som ovan, multiplicerar vi de båda oberoende sannolikheterna tillsammans. I detta sammanhang översätts ordet "och" till multiplikation. Varje flip har en 1/2 chans att landa på huvuden, så vi multiplicerar 1/2 gånger 1/2 för att få 1/4. Det innebär att varje gång vi genomför detta två-flip-experiment har vi en 1/4 chans att få huvuden som resultat. Observera att vi också kunde ha gjort detta problem med decimaler, för att få 0,5 gånger 0,5 = 0,25.
Här är den sista modellfrågan som diskuteras i denna artikel: "Ett rättvist mynt vänds 20 gånger i rad. Vad är chansen att det kommer att landa på huvuden varje gång? Skriv ditt svar med en exponent. " Som vi såg förut har vi att göra med ett "och" villkor för oberoende händelser. Vi behöver den första flipen som huvuden, och den andra flipen är huvuden och den tredje, etc.
Vi måste beräkna 1/2 gånger 1/2 gånger 1/2, upprepade totalt 20 gånger. Det enklaste sättet att representera detta visas till vänster. Det är (1/2) upp till 20: e kraften. Exponenten tillämpas på både täljaren och nämnaren. Eftersom 1 till kraften 20 är bara 1, kan vi också bara skriva vårt svar som 1 dividerat med (2 till 20: e kraften).
Det är intressant att notera att de faktiska oddsna för ovanstående händelse är ungefär en i en miljon. Även om det inte är troligt att någon enskild person kommer att uppleva detta, om du skulle be varje amerikan att göra detta experiment ärligt och korrekt, skulle ett stort antal rapportera framgång.
Eleverna bör se till att de är bekväma att arbeta med de grundläggande sannolikhetskoncept som diskuteras i den här artikeln eftersom de kommer upp ganska ofta.