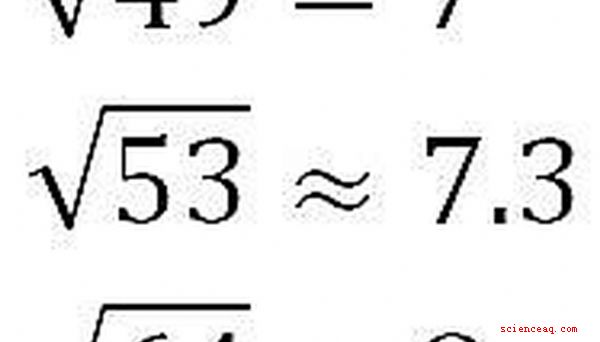
I matematik är det ibland viktigt för oss att kunna beräkna värdena för kvadratrotsar (radikaler). Detta är speciellt fallet på tentor som inte tillåter användning av en kalkylator, och du försöker att eliminera felaktiga svar eller kontrollera rimligheten av ditt svar. I geometri uppträder också värdena sqrt (2) och sqrt (3) så ofta att det är nödvändigt att känna till deras ungefärliga värden.

I den här artikeln visas stegen för att uppskatta en kvadratrots. Artikeln förutsätter att du har en grundläggande förståelse av kvadratrotsar och perfekta rutor. Se referensavsnittet för mer information.

För att uppskatta värdet på kvadratroten av ett tal, hitta de perfekta rutorna ovanför och under siffran. Till exempel, för att uppskatta sqrt (6), notera att 6 ligger mellan de perfekta rutorna 4 och 9. Sqrt (4) = 2 och sqrt (9) = 3. Eftersom 6 är närmare 4 än det är 9, Jag förväntar mig att kvadratroten är närmare 2 än den är 3. Det är faktiskt ca 2,4, men så länge du visste att det var i den här ballparken, skulle du bli bra. Även om du bara vet att det var någonstans mellan 2 och 3 skulle det vara till din fördel.

Låt oss försöka med ett annat exempel. Uppskattning sqrt (53). 53 ligger mellan de perfekta rutorna 49 och 64, vars kvadratrötter är 7 respektive 8. 53 är närmare 49 än till 64, så det skulle vara rimligt att uppskatta sqrt (53) att vara mellan 7 och 7,5. Det visar sig att det handlar om 7,3.

Det finns två fyrkantiga rötter som kommer upp mycket ofta i geometri. De är sqrt (2) och sqrt (3). Det är mycket viktigt att du memorera deras ungefärliga värden. Observera att sqrt (1) är 1 och sqrt (4) är 2. Baserat på detta ska det inte förvånas att sqrt (2) är ungefär 1,4 och sqrt (3) är cirka 1,7.

Det viktigaste är att komma ihåg att sqrt (2) är större än 1, och sqrt (3) är mindre än 2. En annan artikel diskuterar tillämpningen av dessa rötor i arbetet med rätt trianglar och Pythagoras teorem.

Eleverna bör se till att de är bekväma med att uppskatta kvadratrotsnivåer, och för den delen uppskattar alla sina svar för att se om de är rimliga. Detta tillåter dig oftast att fånga dina misstag innan du lämnar in dina tentor.