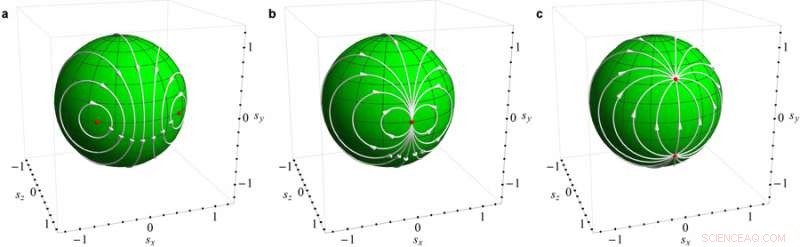
Två Argonne -fysiker erbjöd ett sätt att matematiskt beskriva ett visst fysikfenomen som kallas en fasövergång i ett system ur jämvikt (det vill säga med energi som rör sig genom det) genom att använda imaginära tal. Illustrationen relaterar fasövergången till förändringen mellan matematiska Mobius -transformationer (a, b, och C). Teorin om fysik utanför jämvikt är ett efterlängtat mål på området, och kan så småningom hjälpa oss att designa bättre elektronik. Upphovsman:Vinokur/Galda/Argonne National Laboratory
Inbillade siffror är en lösning på ett mycket verkligt problem i en studie som publicerades idag Vetenskapliga rapporter .
Två fysiker vid US Department of Energy's Argonne National Laboratory erbjöd ett sätt att matematiskt beskriva ett visst fysikfenomen som kallas en fasövergång i ett system ur jämvikt. Sådana fenomen är centrala i fysiken, och att förstå hur de uppstår har varit ett långvarigt och irriterande mål; deras beteende och relaterade effekter är nyckeln till att låsa upp möjligheter för ny elektronik och annan nästa generations teknik.
Inom fysiken, "jämvikt" avser ett tillstånd när ett objekt inte är i rörelse och inte har någon energi som strömmar genom det. Som du kan förvänta dig, de flesta av våra liv sker utanför detta tillstånd:vi rör oss hela tiden och får andra saker att röra sig.
"En regnskur, denna roterande fläkt, dessa system är alla ur jämvikt, "säger studiens medförfattare till Valerii Vinokur, en Argonne Distinguished Fellow och medlem av det gemensamma Argonne-University of Chicago Computation Institute. "När ett system är i jämvikt, vi vet att den alltid har den lägsta möjliga energikonfigurationen, men för icke-jämvikt fungerar inte denna grundläggande princip; och vår förmåga att beskriva fysiken i sådana system är mycket begränsad. "
Han och medförfattaren Alexey Galda, en forskare vid Argonne och University of Chicago James Franck Institute, hade arbetat med sätt att beskriva dessa system, särskilt de som genomgår en fasövergång - till exempel det ögonblick under åskväder när laddningsskillnaden mellan moln och markspetsar är för hög, och ett blixtnedslag inträffar.
De hittade sitt nya tillvägagångssätt för icke-jämviktsfysik i en ny gren av kvantmekaniken. På kvantmekanikens språk, energin i ett system representeras av det som kallas en hamiltons operatör. Traditionellt, kvantmekanik hade ansett att operatören för att representera systemet inte kan innehålla imaginära tal om det skulle betyda att energin inte kommer ut som ett "verkligt" och positivt värde - eftersom systemet faktiskt existerar i verkligheten. Detta tillstånd kallas Hermiticitet.
Men fysiker har tittat hårdare på operatörer som kränker eremititet genom att använda imaginära komponenter, Vinokur sa; flera sådana operatörer som upptäcktes för några år sedan används nu i stor utsträckning inom kvantoptik.
"Vi märkte att sådana operatörer är ett vackert matematiskt verktyg för att beskriva processer som inte är i jämvikt, " han sa.
För att beskriva fasövergången, Galda och Vinokur skrev ut den Hamiltonian operatören, införde en applicerad kraft för att ta den ur jämvikt, och sedan gjorde de kraften imaginär.
"Detta är ett trick som är olagligt ur någon sund förnuftssynpunkt, men vi såg att denna kombination, energi plus imaginär kraft, beskriver matematiskt systemets dynamik med friktion, "Sa Vinokur.
De använde tricket för att beskriva andra fasövergångar utanför jämviktsfasen, såsom en dynamisk Mott -övergång och ett spinnsystem, och såg resultaten överens med antingen observerade experiment eller simuleringar.
I deras senaste arbete, de kopplade sin beskrivning med en operation som kallas en Möbius -transformation, som förekommer i en gren av matematiken som kallas topologi. "Vi kan förstå icke-jämviktsövergångar nu som topologiska övergångar i energirummet, "Sa Galda.
Denna bit av kvantstörning måste förstås djupare, de sa, men är ändå värdefullt; teorin beskriver grundläggande fysikområden som är av stort intresse för nästa generations elektronikteknik.
"För tillfället ser sambandet med topologi ut som matematiskt godis, en vacker sak som vi ännu inte kan använda, men vi vet från historien att om matematiken är tillräckligt elegant, mycket snart följer dess praktiska konsekvenser, "Sa Vinokur.