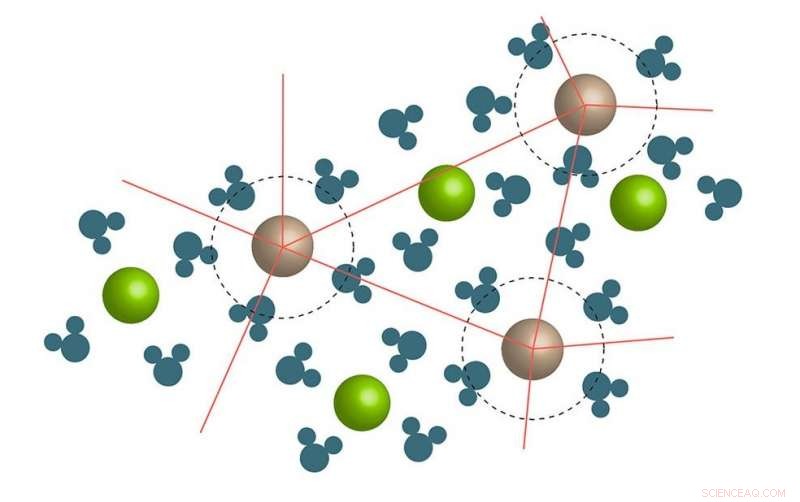
I majonnäs -effekten, en störningsövergång inträffar när en stor mängd löst ämne tillsätts till en lösning. Vid en kritisk lösningskoncentration, rörelsen i jon/vätskeklusterna fryser eller fastnar, vilket gör att viskositeten ökar dramatiskt. Upphovsman:Wynne. © 2017 American Chemical Society
Majonnäs är en stapelvara i nästan varje hushåll, men anledningen till att den är så tjock och trögflytande är ett långvarigt olöst problem inom fysikalisk kemi:varför ökar viskositeten tusen gånger om man lägger till äggula i en rinnande blandning av olja och vatten? Och, mer allmänt, varför uppvisar viskositeten hos alla lösningar en oförutsägbart stor ökning av viskositeten när en stor mängd löst ämne eller ytaktivt ämne (t.ex. äggula) tillsätts?
Jones-Doles ekvation från 1929, som exakt förutspår viskositetsförändringar i lösningar vid lägre koncentrationer, bryts ner vid högre koncentrationer (över 1 molar) som de som finns i sirap och majonnäs. Än så länge, den snabba ökningen av viskositeten vid höga koncentrationer har inte förklarats av vare sig ett matematiskt uttryck eller en mikroskopisk fysikalisk teori.
Nu i en ny studie, Klaas Wynne, professor i kemisk fysik vid University of Glasgow, har föreslagit det han kallar "majonnäseffekten" för att förklara den dramatiska ökningen av viskositeten som inträffar inte bara i majonnäs, men i alla högkoncentrerade lösningar. Hans resultat publiceras i ett nyligen publicerat nummer av Journal of Physical Chemistry Letters .
"" Majonnäs -effekten "är en härlig enkel liten idé som har mycket större tillämpbarhet:i alla fall där en vätska är strukturerad på något sätt, viskositeten kommer att öka olinjärt på grund av närvaron av en virtuell störningsövergång vid en mycket hög koncentration, "Berättade Wynne Phys.org . "Därför, majonnseffekten gäller också för den inneboende strukturen i rumstemperatur joniska vätskor, i djupa eutektiska lösningsmedel, koncentrationsfluktuationer nära kritiska punkter, och naturligtvis flytande blandningar inklusive majonnäs. Majonnseffekten gäller alla lösningar och flytande blandningar, och är därför mycket tillämplig."
I sin tidning, Wynne förklarar hur jamming-övergången uppstår. När ett löst innehållande joner tillsätts till en lösning, flytande molekyler (t.ex. vatten) bildar kluster runt jonerna. Vid en kritisk koncentration, jon/vätskeklusternas rörelse fryser eller fastnar.
Som Wynne förklarar, tillvägagångssättet för denna störningsövergång markerar övergången från regimen som beskrivs av Jones-Dole-ekvationen till en regim där viskositeten ökar mycket snabbare. Majonnäs -effekten, sedan, är ett exempel på en kolligativ egendom, vilket betyder att det främst beror på koncentrationen av det lösta ämnet snarare än på det lösta ämnets kemiska eller fysikaliska egenskaper.
För att matematiskt beskriva viskositetens beroende av koncentration, Wynne har föreslagit modifieringar av Jones-Dole-ekvationen, motiverad av Vogel-Fulcher-Tammann-ekvationen som beskriver viskositeten hos superkylda vätskor och glasögon när de närmar sig den kritiska glasövergångstemperaturen. Wynne visade att den nya modifierade ekvationen ger en bra passform för mycket av de tidigare publicerade viskositetsdata, annat än några förväntade extremvärden. Resultaten visar ett samband mellan glasbildning och majonnäsbildning, som i båda fallen beror viskositeten på koncentrationen på liknande sätt.
I framtiden, Wynne planerar att ytterligare undersöka konsekvenserna av majonnäseffekten.
"Jag är för närvarande enormt intresserad av den fysiska manipulationen av fasövergångar, såsom avblandning av vätskor och kärnbildning av kristaller där majonnäseffekten spelar en viktig roll, sa Wynne.
© 2018 Phys.org