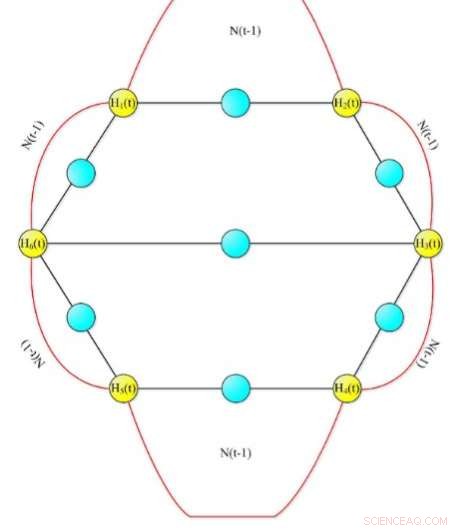
Diagram över den slumpmässiga nätverksmodellen. Kredit:Springer
Nätverk beskrivs ofta som träd med spännande grenar. Hur trädet förgrenas beror på logiken bakom nätverkets expansion, som slumpmässig expansion. Dock, vissa aspekter av sådana slumpmässigt expanderande nätverk är oföränderliga; med andra ord, de har samma egenskaper, oavsett nätverkets skala. Som ett resultat, hela nätverket har samma form som en eller flera av dess delar.
I en ny studie publicerad i EPJ B , Fei Ma från Northwest Normal University i Lanzhou, Gansu-provinsen, Kina, anc-kollegor beräknar det totala antalet spännande träd i slumpmässigt expanderande nätverk. Denna metod kan användas för att modellera skalfria nätverksmodeller, som, som det visar sig, kännetecknas av små världsfastigheter. Detta betyder, till exempel, att medlemmar i nätverket endast uppvisar sex grader av separation, som de flesta i vårt samhälle.
Tidigare, ett antal nätverksmodeller baserades på grafer som bestod av en aggregering av hörn med sammanbindande kanter. Men de var inte tillräckliga för att modellera verkliga nätverk, som nätverk av användare av sociala medier. Istället, komplexa nätverk, där nätverket skapas slumpmässigt, har blivit grundpelarna i datavetenskap och modern diskret matematik. Använda data från verkliga nätverk, och att dra nytta av erfarenheterna från konstgjorda nätverk som skapats för att redogöra för specifika funktioner, författarna designar mer realistiska modeller som är mer komplexa än sina föregångare.
I den här studien, författarna fokuserar på att utveckla en rekursiv metod för att beräkna antalet spännande träd i ett nätverk, vilket är särskilt användbart för att förutsäga dess förmåga att tolerera fel som uppstår slumpmässigt. Att kunna hitta antalet spännande träd i nätverksmodeller har implikationer för olika vetenskapliga områden, som tillämpad matematik, teoretisk datavetenskap, fysik och kemi.