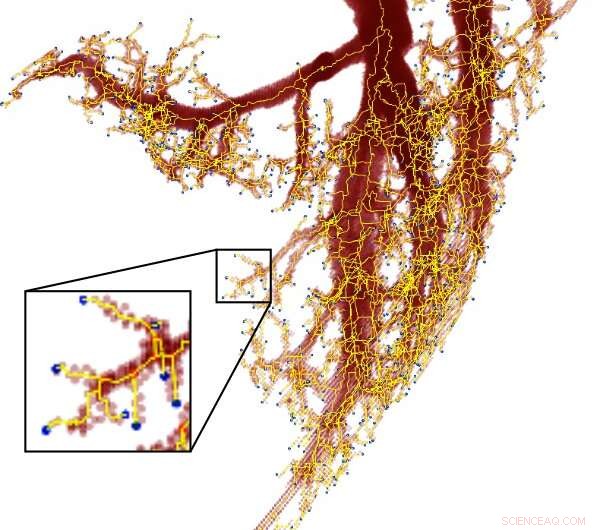
Eftersom venerna förgrenar sig i ungefär proportionella divisioner, de anses också vara en fraktal. Upphovsman:Courtesy image/Mitchell Newberry
Jätte jordbävningar och extrem rikedom verkar inte ha mycket gemensamt, men hur ofta "den stora" kommer att träffa San Francisco och hur ofta någon kommer att tjäna lika mycket pengar som Bill Gates kan båda förutses med en statistisk mätning som kallas en power law -exponent.
Under förra seklet, forskare har använt vad som kallas en maktlag för att förutsäga vissa typer av händelser, inklusive hur ofta jordbävningar vid vissa punkter på Richterskalan kommer att inträffa. Men en forskare från University of Michigan märkte att denna kraftlag inte passar alla omständigheter.
Mitchell Newberry, en Michigan-stipendiat och biträdande professor vid UM Center for the Study of Complex Systems, föreslår en justering av maktlagen som skulle redogöra för händelser som ökar eller minskar i fasta proportioner - till exempel när en chef gör ungefär 20 procent mer än sin anställd.
Dessa justeringar påverkar hur man uppskattar sannolikheten för jordbävningar, antalet kapillärer i människokroppen, och storleken på megastäder och solfacklor. Och de kanske reviderar när de kan förvänta sig nästa stora.
När forskare plottar något liknande sannolikheten för extrem rikedom på ett diagram, kurvan är en slät linje. Det beror på att människor kan ha hur mycket pengar som helst på sina bankkonton.
"Denna kurvas jämnhet innebär att valfritt värde är möjligt, "Sa Newberry." Jag kunde tjäna ett öre mer lika lätt som ett öre mindre. "
Det är inte exakt fallet med händelser som jordbävningar på grund av hur de registreras på Richters skala. Richterstorleken på jordbävningar ökar eller minskar i steg om 0,1, exponentiellt. En jordbävning med storleken 3,1 är 1,26 gånger så kraftfull som jordbävningarna med magnitud 3,0, så inte alla värden är möjliga på skalan. Richterskalan är ett exempel på ett begrepp som kallas "självlikhet, "eller när en händelse eller sak är gjord av proportionellt mindre kopior av sig själv.
Du kan se självlikhet i naturen som förgrening av vener i ett blad, eller i geometri som passande trianglar inom större trianglar med samma form, kallas en Sierpinski triangel. Så, att redogöra för händelser som ändras i exakta proportioner, Newberry och hans medförfattare Van Savage från University of California, Los Angeles, konstruerade den diskreta maktlagen.

Koch -kurvan upprepar sig oändligt, visar självlikhet. Upphovsman:Wikimedia -användare Leofun01
I dessa maktlagsekvationer, exponenten i ekvationen är den variabel forskare löser för. I jordbävningar, den exponenten, kallade Gutenberg-Richter b-värdet, mättes första gången 1944 och indikerar hur ofta en jordbävning med en viss styrka sannolikt kommer att inträffa. Newberrys diskreta kraftlag gav en korrigering på 11,7% över uppskattningar baserade på den kontinuerliga kraftlagen, föra exponenten närmare i linje med den historiska frekvensen av stora jordbävningar. Till och med en 5% -korrigering innebär en mer än tvåfaldig skillnad i när man kan förvänta sig nästa gigantiska jordbävning.
"I 100 år, människor har pratat om ungefär en typ av maktlagsfördelning. Det är maktlagens fördelning av rikedom och jordbävningar, "Sa Newberry." Först nu, vi dokumenterar dessa diskreta skalor. Istället för en jämn kurva, vår maktlag ser ut som en oändlig trappa. "
Newberry märkte bristen i den kontinuerliga kraftlagen i sin studie av cirkulationssystemets fysik. Cirkulationssystemet börjar med ett stort blodkärl:aorta. När aortan delas upp i olika grenar-halspulsådern och subklavian artärer-minskar varje ny gren i diameter med ungefär två tredjedelar.
Han använde den kontinuerliga kraftlagen för att uppskatta storleken på blodkärl när de fortsätter att förgrena sig. Men kraftlagen gav storlekar på blodkärl som inte kunde förekomma. Det indikerade att ett blodkärl bara kan vara något mindre än stammen från vilken det förgrenade sig istället för cirka två tredjedelar av stammens storlek.
"Med hjälp av den kontinuerliga maktlagen, vi fick bara svar som vi visste var fel, "Sa Newberry." Genom att felsöka det som misslyckades, vi kom på att denna fördelning gör antagandet att varje blodkärlstorlek är lika trolig. Vi vet att för verklig kärl, så är det inte. "
Så Newberry omvandlade kraftlagen. Genom att titta på blodkärl, Newberry kan härleda kraftlagsexponenten från två konstanter:hur många grenar vid varje korsning - två - och hur mycket mindre varje gren är i förhållande till stammen. Mät fartygsstorlekar vid varje division, Newberry kunde lösa för distributionen av blodkärlen.
"Det finns en mellanväg mellan en kontinuerlig maktlag och den diskreta maktlagen, "Sa Newberry." I den diskreta maktlagen, allt är upplagt i perfekt styva proportioner från den högsta skalan till det oändligt små. I lagen om kontinuerlig makt, allt är helt slumpmässigt upplagt. Nästan allt självliknande i verkligheten är en blandning av dessa två. "
Newberrys studie publiceras i tidskriften Fysiska granskningsbrev .