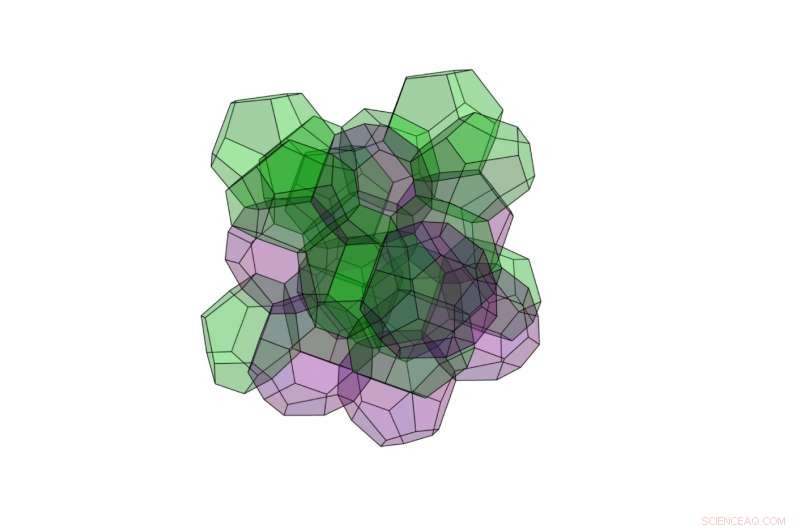
En av de nya 3D-strukturerna har den lägsta ytan av någon känd rymddelningsstruktur:den är gjord av 24 polyeder, varav några har 12 ansikten och några har 16 ansikten. Eftersom polyederna med 12 och 16 ansikten här har olika volymer, den nya strukturen uppfyller inte Kelvins ursprungliga krav på lika stora volymer. Kredit:Opsomer och Vandewalle. © 2016 IOP Publishing
(Phys.org) —Forskare har upptäckt en ny 3D -struktur som delar rymden i 24 regioner, och har visat att det är den bästa lösningen ännu på en modifierad version av ett geometriskt rymdpartitionsproblem som har utmanat forskare i mer än ett sekel.
År 1887, Lord Kelvin frågade hur rymden kunde delas in i 3D -strukturer med samma volym på ett sätt som minimerar den totala ytan för varje struktur. Det måste vara möjligt att tätt packa ihop många av dessa strukturer utan några mellanrum mellan dem - med andra ord, de måste vara "rymdfyllande" strukturer. Varje struktur kan anta en mängd komplexa 3D -former, eller "polyeder, "antingen som en enda polyeder eller en kombination av flera mindre polyeder av olika typer. Utmaningen är att ta reda på vilka särskilda typer av polyeder som ska användas för att minimera den yttre ytan av hela strukturen.
Kelvins bästa lösning på detta problem var en enda polyeder som kallas en "tetrakaidecahedron, "som har 14 ytor:sex rutor och åtta hexagoner. Eftersom detta är formen som erhålls när man skär av hörnen av en 3D -diamantform, den kan också ses som en stympad oktaeder.
Även om Kelvins lösning varade i mer än ett sekel, 1994 använde Denis Weaire och Robert Phelan vid Trinity College Dublin numeriska simuleringar för att upptäcka en mer optimal rymdpartition. Weaire och Phelans lösning är gjord av åtta polyeder av två olika typer, även om båda typerna har samma volym:sex av Kelvins tetrakaidecahedron och två dodecahedron (som har 12 ansikten). Tillsammans, dessa åtta polyeder utgör en 3D -struktur som har 0,3% mindre ytarea än Kelvins enda tetrakaidecahedron. Weaire-Phelan-strukturen har förblivit den mest optimala lösningen på Kelvins problem under de senaste 22 åren.
Nu i den nya studien, fysikerna Eric Opsomer och Nicolas Vandewalle vid University of Liége i Belgien har utvecklat en ny algoritm för att hitta rymdfyllande komposit polyhedrala strukturer med minimal ytarea.
Med den nya metoden, de upptäckte att en ny 3D-struktur gjord av 24 polyeder har en ännu lägre ytarea än Weaire-Phelan-strukturen. De 24 polyedrarna är av två olika typer:vissa har 12 ansikten och några har 16 ansikten. Till skillnad från Weaire-Phelan-strukturen, där de två olika typerna av polyeder har lika stora volymer, 12- och 16-fasade polyeder här har betydligt olika volymer. Av denna anledning, den nya strukturen uppfyller inte Kelvins ursprungliga krav på lika stora volymer.
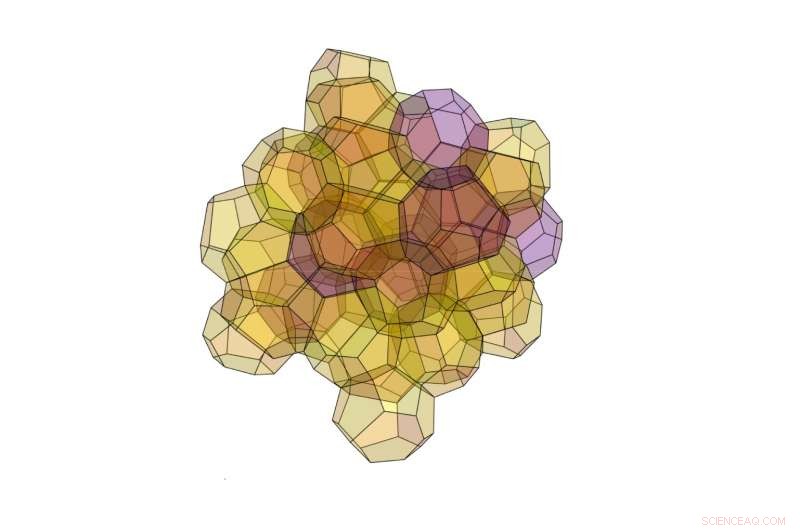
Den nya algoritmen avslöjade denna 3D -struktur bestående av 40 polyeder av två olika typer. Kredit:Opsomer och Vandewalle. © 2016 IOP Publishing
"Tyvärr, det är ingen riktig lösning, 'eftersom celler med lika volym är ett krav för det ursprungliga Kelvin -problemet, "Berättade Opsomer Phys.org . Ändå, strukturen är fortfarande intressant av andra skäl. "Dessa resultat kan leda till upptäckten av strukturer med potentiella konsekvenser för materialfysik, medicinsk forskning, och andra områden, "Sa Opsomer.
Som forskarna förklarade, de avsiktligt tog bort begränsningen av lika volymer när de utvecklade sin sökmetod eftersom det tillät dem att utforma algoritmen på ett nytt sätt:istället för att direkt minimera ytan på en struktur, de maximerade polyhedras genomsnittliga isoperimetrar (perimeterna som delas av alla intilliggande polyeder). Även om dessa två tillvägagångssätt är olika, de är i slutändan likvärdiga.
Forskarna använde den nya algoritmen för att utforska flera 3D -strukturer gjorda av mellan två och 64 polyeder. Börjar med ett specifikt antal slumpmässigt arrangerade punkter i 3D -utrymme, algoritmen börjar flytta runt punkterna. Efter varje iteration, algoritmen beräknar den nya genomsnittliga isoperimetern, och baserat på resultatet antingen behåller eller avvisar den nya konfigurationen med en viss sannolikhet. Efter miljoner och ibland miljarder iterationer, punkterna bildar så småningom hörnen på flera polyeder som tillsammans bildar en 3D -struktur med mycket låg ytarea.
Eftersom det för närvarande inte finns något sätt att bevisa vad den mest optimala rymddelningsstrukturen är (med eller utan celler med lika volym), forskarna planerar att fortsätta söka efter en mängd olika strukturer av alla slag. Deras bästa gissning är att det finns ännu mer optimala strukturer, och de planerar att använda sin algoritm för att fortsätta sin utforskning.
Forskarna förväntar sig också att algoritmen kan generera andra unika strukturer. En särskilt intressant struktur de upptäckte här är en 40-polyederstruktur som är mer optimal än Kelvins struktur men inte riktigt lika bra som Weaire-Phelan-strukturen. Denna mycket komplexa struktur är också ovanlig genom att den inte tillhör en kategori av strukturer som kallas Frank-Kasper-strukturer, som forskare traditionellt har fokuserat på för optimal rymdpartitionering. Fyndet tyder på att andra optimala strukturer också kan existera utanför denna kategori.
Även om Kelvins problem ursprungligen inte föreslogs att tillgodose något praktiskt behov, optimal rymdpartitionering har nu en mängd olika applikationer. På det medicinska området, dessa begrepp har använts för att designa starka, lätta benvävnadsersättningar. Optimal rymdpartitionering har också inspirerat arkitektur, med ett anmärkningsvärt exempel är simplatsen som byggdes för OS i Peking 2008. Byggnaden, som kallas vattenkuben, är baserad på Weaire-Phelan-strukturen.
© 2016 Phys.org