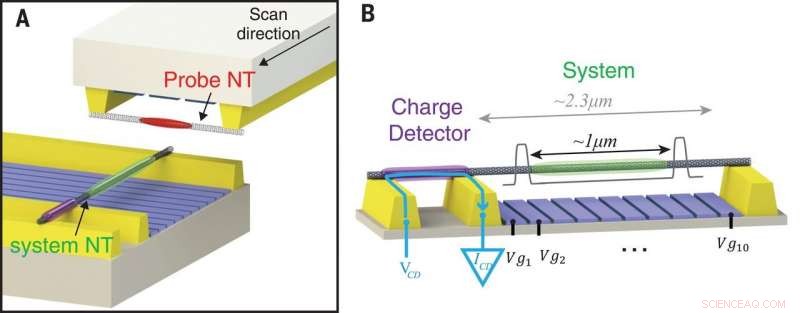
Experimentell plattform för avbildning av starkt interagerande elektroner. (A) Inställning av skanningssond bestående av två kolnanorör (NT) -enheter-en system-NT-enhet (botten) som är värd för elektronerna som ska avbildas (grön ellips) och en sond-NT-enhet (upptill) som innehåller sonderande elektroner (röda ). I experimentet, sonden NT skannas längs system -NT (svart pil). (B) Systemet NT är anslutet till kontakter (gult) och hänger över 10 grindar (blå) som används för att skapa en potentiell brunn (visad schematiskt i grått) som begränsar några elektroner till den mellersta delen av den upphängda NT (grön) , borta från kontakterna. Tillägget av dessa elektroner detekteras med en laddningsdetektor - en separat kvantpunkt bildad på ett sidosegment av samma NT (lila). Detektorn är förspänd av en spänning, VCD, appliceras på en extern kontakt, som leder till en ström, ICD, flödar endast mellan laddningsdetektorns kontakter (blå pil), så att ingen ström passerar genom huvuddelen av systemet NT. Kredit:Vetenskap, doi:10.1126/science.aat0905
När elektroner som stöter bort varandra är begränsade till ett litet utrymme, de kan bilda ett ordnat kristallint tillstånd som kallas en Wignerkristall. Det är svårt att observera den ömtåliga kristallen, eftersom det kräver extrema förhållanden inklusive låga temperaturer och densiteter, såväl som icke -invasiva bildprober. För att övervinna de utmanande bildförhållandena, I. Shapir och ett forskargrupp vid avdelningarna för fysik och kondenserad materiefysik i Israel, Rumänien och Ungern skapade förutsättningar i ett kolnanorör (NT) för att hysa elektronerna. De följde detta experimentella steg genom att använda en andra nanorör som en sond (kallad "sond NT") för att skanna den första nanoröret (kallad "system NT"). Fysikerna mätte de elektroniska densiteterna och visade sin överensstämmelse med teoretiska förutsägelser för att visa små Wignerkristaller med upp till sex elektroner i en dimension (1-D). Resultaten publiceras nu i Vetenskap .
För mer än 80 år sedan, fysikern Eugene Wigner förutspådde elektronernas kvantkristall, som fortfarande är ett av de mest svårfångade tillstånden. I det nuvarande arbetet, Shapir och medarbetare utvecklade en teknik för att direkt avbilda Wignerkristallen i 1-D genom att avbilda dess laddningstäthet i verkligt utrymme. De fick bilder av några elektroner begränsade i 1-D som matchade de teoretiska förutsägelserna för starkt interagerande kristaller. Forskarna tittade på kristallens kvantkaraktär med hjälp av kollektiv tunnel genom en elektrisk potentialbarriär begränsad med elektriskt oberoende grindar. Arbetet gav direkt bevis för bildandet av små Wignerkristaller, banar väg för att studera ömtåliga interagerande tillstånd hos elektroner genom att avbilda deras mångkroppstäthet i det verkliga rummet.
I hans 1934 -papper, fysikern Eugene Wigner förutspådde att när långsiktiga Coulomb-interaktioner i ett elektronsystem dominerade den kinetiska energin och störningen, de skulle dyka upp i ett kristallint grundtillstånd. Där elektronerna hölls isär oavsett kvantantal. Experimentella fysiker började söka efter denna kvantkristall i de renaste tillgängliga elektroniska systemen därefter, inklusive flytande helium och lågdimensionella halvledar heterostrukturer.
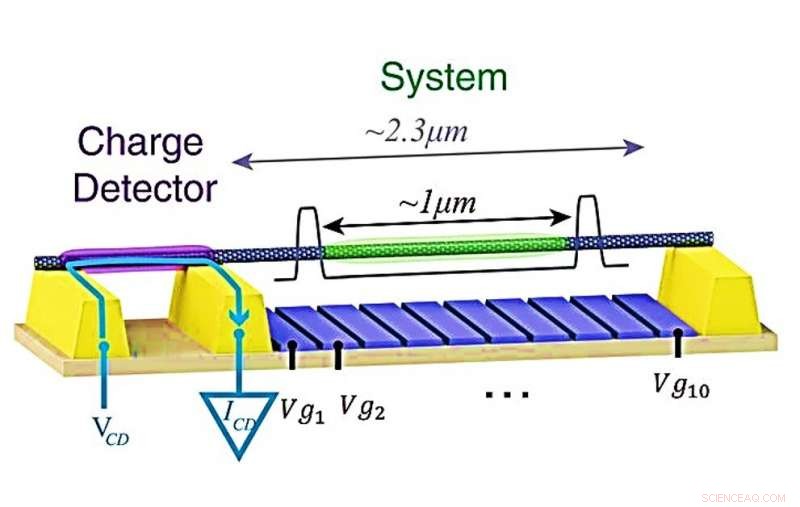
Experimentell plattform för att avbilda Wignerkristallen. Systemet NT är anslutet till kontakter (gult) och hänger över 10 grindar (blå) som används för att skapa en potentiell brunn (visad schematiskt i grått) som begränsar några elektroner till den mellersta delen av den upphängda NT (grön), borta från kontakterna. Tillägget av dessa elektroner detekteras med en laddningsdetektor - en separat kvantpunkt bildad på ett sidosegment av samma NT (lila). Detektorn är förspänd av en spänning, VCD, appliceras på en extern kontakt, som leder till en ström, ICD, flödar endast mellan laddningsdetektorns kontakter (blå pil), så att ingen ström passerar genom huvuddelen av systemet NT. Kredit:Vetenskap, doi:10.1126/science.aat0905.
Fysiker hade tidigare utfört mätningar i tvådimensionella (2-D) elektroniska system i förhållande till transport, mikrovågsfält, Nukleär magnetisk resonans, optisk, tunnelsystem och tvåskikts elektronsystem för att indikera förekomsten av en kristall vid höga magnetfält. Observera ett kristallint tillstånd i en-dimension (1-D), i ett oändligt system är oväntat, eftersom termiska och kvantfluktuationer kan förstöra långdistansordning. Dock, i ändliga system, fysiker hade studerat det teoretiska endimensionella Wignerkristalltillståndet sedan den kvasi långdistansordnade orden gav kristallina korrelationer. Experimentella fysiker följde denna observation med experimentell sondering via transportmätningar, men experimenten kunde bara undersöka makroskopiska egenskaper hos detta tillstånd.
I princip, ett lämpligt bildverktyg krävs för att observera det entydiga fingeravtrycket hos en Wignerkristall i dess verkliga rymdstruktur. Forskare använde därför skanningssondförsök, även om de bara kunde avbilda det icke-interagerande tillståndet eller visa invasiv grindning av sonden. Mätningarna belyste den inneboende svårigheten att avbilda elektroninteraktioner med konventionella skanningsmetoder. För att individuellt lösa och identifiera elektroner, en makroskopisk, metallisk eller dielektrisk spets bör närma sig elektronerna närmare än deras ömsesidiga separation. Ändå, sådana tips och deras interaktioner kan starkt snedvrida tillståndet som studeras. Forskare krävde därför en annan skanningssond för att avbilda ett interagerande tillstånd eller elektronsystem.

Real-space avbildning av densitetsprofilen för en enda begränsad elektron. (A) För att avbilda densitetsfördelningen för en enda elektron begränsad i en potentiell "låda" (grå), vi lägger en fast laddning i sonden NT och skannar den över systemet NT. Denna laddning skapar en lokal störning vid sondpositionen xprobe (röd), som förskjuter marktillståndsenergin för systemelektronen, E1 (toppaneler), proportionell mot den lokala densiteten vid sondpositionen E1 (xprobe) ~ ρ1 (xprobe). Genom att mäta den globala grindspänningen, Vg, behövs för att hålla laddningen av denna enda elektron i resonans med ledningarnas Fermi -energi, EF, för varierande xprobe (bottenpaneler), forskarna spårar effektivt profilen för dess laddningsfördelning Vg (xprobe) ~ ρ1 (xprobe). (B) Derivat av laddningsdetektorström med avseende på Vg, dICD/dVg, mätt som en funktion Vg. Den skarpa laddningstoppen motsvarar att den första elektronen kommer in i system-NT-potentialbrunnen (i fig. 3, de gröna och röda etiketterna anger antalet elektroner i systemet respektive i sonden). a.u., godtyckliga enheter. (C) dICD/dVg som en funktion av Vg och xprobe. Laddningsresonansen spårar en kurva som ger laddningstätheten hos elektronen som är sammanblandad med sondens punktspridningsfunktion. (Insatser) Illustration av systemet och sondenheter för olika mätpositioner. (D) Samma som i (C), men för olika sondladdningar från qprobe =0e till 3e. (E) Spåren extraherade från panel (D), ritade ihop. Kredit:Vetenskap, doi:10.1126/science.aat0905.
I det nuvarande arbetet, Shapir et al. introducerade en skanningssondplattform som använde en kolnanorör (NT) som en mycket känslig, men ändå minimalt invasiv skanningssond för att se mångkroppstätheten hos starkt interagerande elektroner. Plattformen innehöll ett specialtillverkat skanningsmikroskop som arbetar vid kryogena temperaturer (~ 10 mK) där två motsatta NT-enheter kunde föras i närheten och skannas längs varandra. Forskarna använde en enhet för att vara värd för system-NT som 1-D-plattformen som studeras, och den andra anordningen vinkelrätt mot den som innehåller sonden NT. De monterade de två enheterna med hjälp av en nano -monteringsteknik för att bilda orörda NT -enheter som hängde ovanför en rad metalliska grindar.
Forskarna upprätthåller avgörande starka interaktioner och låg störning i systemet för att erhålla en Wignerkristall genom att hänga upp NT:erna långt över metallportarna vid 400 nm. Sedan använde de 10 elektriskt oberoende grindar en potential som begränsade elektronerna mellan två barriärer 1 µm från varandra, lokalisera dem centralt i en lång hängande nanorör, borta från kontakter för att förhindra oönskade interaktioner.
Shapir et al. använde mycket ogenomskinliga barriärer för att förhindra hybridisering av den begränsade elektronens vågfunktion med elektronernas i resten av NT. Eftersom transporten i denna situation var starkt undertryckt, forskarna undersökte de begränsade elektronerna med hjälp av en laddningsdetektor som finns på ett separat segment av samma NT. Sonden NT -enhet separat som användes i studien upprätthöll en nästan identisk struktur, som endast skilde sig med upphängningslängden på 1,6 µm och antalet grindar (tre).
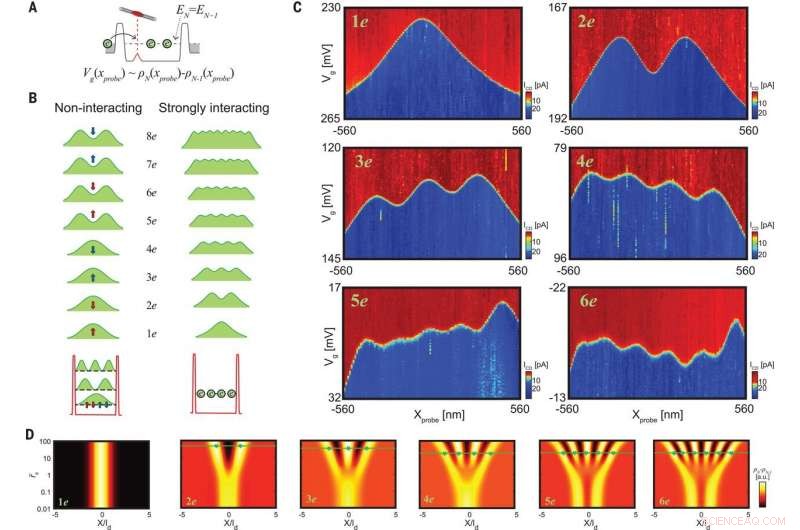
:Avbildning av differentialtätheten hos många elektrontillstånd. (A) I en laddningsövergång från N - 1 till N elektroner, resonansen inträffar för EN =EN – 1 och grindspänningsförskjutningen avbildar differensdensiteten Vg (xprobe) ~ ρN (xprobe) - ρN - 1 (xprobe). (B) Illustration av den förväntade differensdensiteten hos icke -interagerande (vänster) kontra starkt interagerande (höger) elektroner i en kol -NT. Dessa skisser inkluderar också den slutliga upplösningen. Icke-interagerande elektroner upptar partikel-i-en-lådans vågfunktioner, var och en är fyrfaldig degenererad på grund av snurr och dal degenerering (röda och blå pilar). Följaktligen, differentialtätheten för de fyra första elektronerna bör vara identisk och enkel, och de av de fyra kommande bör vara dubbla. För fallet med starkt samverkan, elektronerna separerar i verkligt utrymme (nere till höger), och varje tillsatt elektron kommer att lägga till ytterligare en topp till differensdensitetsprofilen (uppe till höger). (C) Mätning av ICD som en funktion av Vg och xprobe, runt laddningstopparna för de första sex elektronerna i systemet. Kurvorna spårar direkt differentialtätheten hos dessa många elektrontillstånd, visar att de är djupt inne i den starkt interagerande regimen. (D) differensdensiteten för de första sex elektronerna, beräknat med DMRG, som betraktar långsiktiga elektroniska interaktioner som en funktion av den rumsliga koordinaten x/ld och den effektiva styrkan hos elektroniska interaktioner, rs, allt från mycket svag (r˜s =0,01) till mycket stark (r˜s =100). Gröna stjärnor markerar positionerna för topparna mätt i experimentet, och de gröna linjerna markerar de beräknade positionerna (med en enda ledig parameter ld =160 nm). Kredit:Vetenskap, doi:10.1126/science.aat0905.
Forskarna demonstrerade arbetsprincipen bakom bildtekniken som kallas "skanningsladdning, "börjar med de enklaste experimenten för att avbilda laddningsfördelningen för en enda elektron som är begränsad i en 1-D-låda. Shapir et al. mätte systemets energiska svar på en skannad störning (agitation) och bestämde direkt systemets densitetsfördelning. Av mäta systemets energi som en funktion av sonden NT, forskarna löste direkt elektronens densitetsprofil. När man mäter energin, forskarna hänvisade det till Fermi -energin i ledningarna och krediterade störningen som producerades av sonderna till separationen mellan de två NT:erna och till den begränsade laddningen i sonden NT.
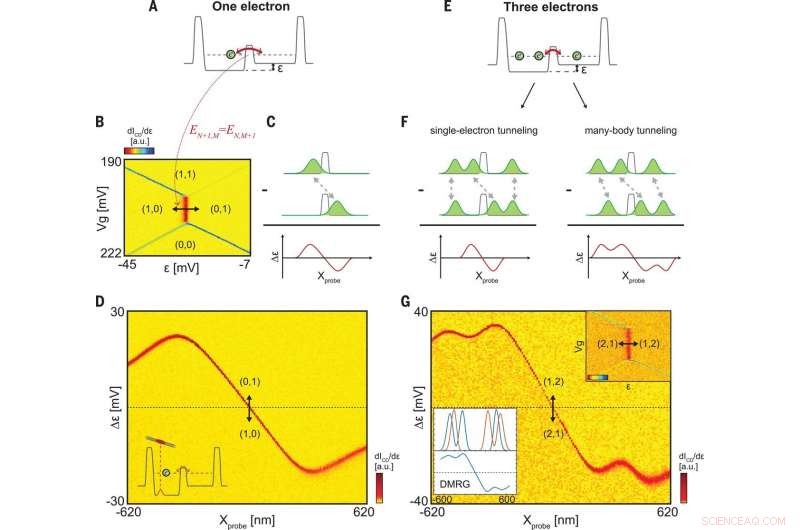
Tunnel med många kroppar av fåelektrontillståndet. (A) Illustration av det potentiella landskapet, som nu innehåller en central barriär genom vilken en elektron kan tunnel (röd pil). Avstängningsspänningen, ε, ändrar den relativa höjden på botten i varje brunn. (B) Laddningsstabilitetsdiagram för 1e som funktion av Vg och ε, mätt med dICD/dε (färgfält). Staterna (N, M) betecknar laddningen N (M) i de vänstra (höger) brunnarna. Den vertikala, bredare linje motsvarar en intern tunneling, inträffar när EN+1, M =EN, M+1. (C) Schematisk över den förväntade tunneldifferentialdensiteten för en elektron (röd "dipol", botten), givet av skillnaden mellan dess densitetsfördelning före och efter tunnelföring [ρ10 (x) och ρ01 (x)] som är inblandad i sondens punktspridningsfunktion (PSF). (D) Uppmätt laddningsdetektorsignal som funktion xprobe och skillnaden i avstämning i förhållande till det ostörda tillståndet, Δε. Det röda spåret visar Δε (xprobe) som är nödvändig för att hålla tunneln i resonans (visas schematiskt i infälld), vilket ger tunneldifferentiell densitet. (E) Samma som (A), men för tre elektroner i fällan. (F) Två scenarier för tunneln:(vänster) Endast den centrala elektronen rör sig i tunnelhändelsen; Δε (xprobe) visar en enda dipol, som i ettelektronfallet som illustreras i (C). (Höger) Tunnel med många kroppar, där koordinaterna för alla elektroner rör sig koherent i tunnelprocessen; flera dipoler förväntas i differentialtunnelsignalen. (G) (Övre insats) Laddningsstabilitetsdiagram över tre elektroner, med ICD/dε (a.u.) uppmätt för −42 mV <ε <10 mV, 170 mV
Shapir et al. erhöll sex paneler i experimenten för att indikera differensdensiteten för de sex elektroner som tillförts systemet NT. För minimala störningar, de utförde alla skanningar med en elektron i sonden NT. De avbildade densitetsprofilerna skilde sig klart från de som förutses av enpartikelfysik men matchade dem med en starkt samverkande kristall. När Shapir et al. ökat antalet elektroner, elektronavståndet minskat, även om deras totala hastighet ökade för att beteckna elektroner begränsade i en "låda" med mjuka väggar. De resulterande bilderna gavs direkt, realtidsobservationer av de elektroniska Wignerkristallerna.
För att kvantitativt förstå mätningarna, Shapir et al. utförde beräkningar av densitetsmatrisrenormaliseringsgrupp (DMRG) och inkluderade Coulomb-interaktioner över långa avstånd. De uppmätta elektronpositionerna (betraktade som gröna stjärnor) överensstämde väl med de som förutspås av DMRG, placera de observerade kristallerna väl inom den starkt interagerande regimen i den experimentella inställningen. För att förstå Wignerkristallens kvantkaraktär, Shapir et al. mätte kristallens tunnelfunktioner och förväntade sig att korrelationerna mellan elektronerna i en kristall skulle få kristallen att tunnla genom en barriär kollektivt. De såg att tunneldifferensdensiteten blev mer intressant i ett system med mer än en elektron eftersom den visade direkta fingeravtryck av kollektiv rörelse.
På det här sättet, Shapir et al. använde en ny metod för att direkt avbilda den rumsliga ordningen av interagerande elektroner. Baserat på resultaten, de förutser möjligheten att ta upp ytterligare grundläggande frågor relaterade till kvantelektronisk kristall, inklusive arten av dess magnetiska ordning. Skanningsplattformen utvecklad av Shapir et al. kommer att möjliggöra ytterligare utforskning av ett mycket brett spektrum av kanoniska interagerande elektrontillstånd i materia som tidigare var bortom bildavstånd.
© 2019 Science X Network