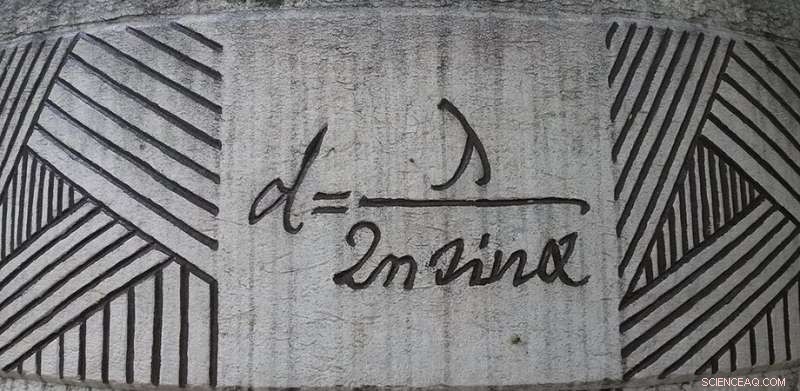
Ernst Abbes diffraktionsekvation som visas i Jena, Tyskland. Upphovsman:Daniel Mietchen, Wikimedia, commons.wikimedia.org/wiki/File:Ernst-Abbe-Denkmal_Jena_F%C3%BCrstengraben_-_20140802_125709.jpg
Även om vi får veta att en bild talar tusen ord, att klyschan allvarligt underskattar värdet av en bra bild. Vår förståelse för hur världen fungerar förenklas av vår förmåga att förvandla data till bilder. Imaging är kärnan i vetenskapen:om det kan mätas, det kommer att förvandlas till en bild som ska analyseras.
Den begränsande faktorn för bildbehandling är upplösning. Hur nära kan två objekt vara innan ett bildsystem reducerar dem till en enda suddig plats? Den frågan besvarades först av Ernst Abbe 1873. Han teoretiserade att om två objekt är närmare än ungefär en halv våglängd, de kan inte lösas. Abbe fick sin gräns genom att överväga hur diffraktion med ett objektiv skulle suddas ut en punktkälla.
I ungefär ett sekel, Abbes diffraktionsgräns togs som en vetenskaplig sanning. Säker, du kan spela några spel med det lysande ljuset och bildmediet för att få en faktor två eller tre, men faktorer på tio eller 100 var ofattbara. Det har nu förändrats, med många bildtekniker som kan lösa bortom Abbes diffraktionsgräns, som nu ligger krossat i hörnet av vetenskapens verkstad under skuggan av två nobelpriser. Men finns det fortfarande en gräns? Hur nära kan två föremål vara innan de suddas ut på en enda plats? Detta är den fråga som Evgenii Narimanov från Purdue University har försökt svara på i en nyligen Avancerad fotonik papper.
Deblurring imaging
När det gäller bildbehandling, det är mycket enklare att lägga undan begreppet diffraktion och istället tänka på information. När ett objekt avbildas, ljus sprids av objektet mot bildsystemet. Det rumsliga mönstret, eller information, av bilden bärs av ljusets rumsliga frekvenser. För att återställa en korrekt bild, bildsystemet måste överföra dessa rumsfrekvenser utan att ändra dem. Men, varje system har sina gränser, så vissa rumsfrekvensers bidrag kommer att gå förlorade.
Den resulterande bilden görs genom rekombination av de rumsfrekvenser som överförs av bildsystemet. Om bildsystemet inte kan sända frekvenser över en viss gräns, då kommer bilden inte att innehålla den informationen, vilket resulterar i suddighet. Om du anser att bildsystemet kan överföra rumsfrekvenser upp till en gränsfrekvens, men kan inte sända frekvenser över gränsen, då blir den resulterande bildupplösningen exakt som Abbe förutspådde (men med enklare matematik).
Verkligen, informationen som överförs av ett bildsystem beskrivs av exakt samma matematik som används av ingenjörer som studerar överföring av data ner till telefonkablar, som gör det möjligt att använda informationsteoriens verktyg för att förutsäga bildsystemens prestanda.
Avkodning av meddelanden i en bild
Narimanov har gått ett steg längre i att abstrakta bildprocessen genom att bara överväga informationsöverföring, oberoende av hur informationen kodas. När det är gjort, en bilds upplösning bestäms endast av den ömsesidiga informationen som delas mellan objektet och bilden. I denna ram, som är oberoende av alla funktionella detaljer, upplösningsgränsen ges av det buller som introduceras under informationsöverföring. I praktiken beror bruset på detektorn, ljusspridning, fluktuationer i belysningsförhållanden, och många fler detaljer.
Genom att ta detta abstrakta tillvägagångssätt, Narimanov kunde ta fram en teori som förutsäger bästa möjliga upplösning för en bild endast baserat på förhållandet mellan signalstyrkan och brusmängden. Ju högre signal / brusförhållande, desto bättre möjlig upplösning.
Utnyttja denna teori, papperet innehåller också ett antal beräkningar för mer specifika bildsystem, som de som använder strukturerad belysning, och för avbildning av glesa föremål, som har få funktioner ofta klumpade ihop. Möjligheterna att förbättra en bild med efterbearbetning diskuteras också:vi är alla bekanta med tv -brottsdrama som verkar kunna förbättra bilderna efter behag. Även om detta inte är möjligt som visas på TV, det finns ett inslag av sanning. Giltiga metoder för beräkningsmässig efterbehandling av en bild kan avslöja några dolda detaljer. Denna teori visar gränserna för detta tillvägagångssätt, för.
Narimanovs tillvägagångssätt avslöjar inte vilken aspekt av ett system som för närvarande begränsar upplösningen. För det, mer specifika modeller krävs fortfarande. Istället, det är bättre att tänka på Narimanovs modell som en vägledning:var är de största vinsterna i upplösning att hitta för minst ansträngning? Den informationen är användbar när du bestämmer var du ska investera tid och pengar.