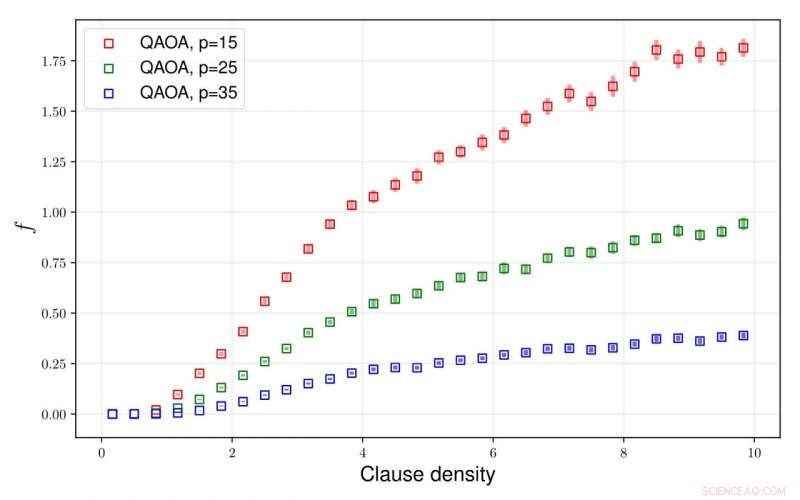
Grafen representerar prestandan (skillnaden mellan QAOA-optima och exakta optima) för QAOA-kretsar med fast djup på slumpmässigt genererade MAX-SAT-instanser med ökande problemdensiteter. Även om versioner med högre djup uppnår bättre prestanda, de uppvisar fortfarande brister i tillgänglighet. Kreditera: Fysiska granskningsbrev
Google tävlar för att utveckla kvantförbättrade processorer som använder kvantmekaniska effekter för att öka hastigheten med vilken data kan bearbetas. På kort sikt, Google har tagit fram nya kvantförbättrade algoritmer som fungerar i närvaro av realistiskt brus. Den så kallade kvantapproximativa optimeringsalgoritmen, eller QAOA för kort, är hörnstenen i en modern strävan mot brustolerant kvantförstärkt algoritmutveckling.
Det berömda tillvägagångssättet av Google i QAOA har väckt ett stort kommersiellt intresse och väckt ett globalt forskarsamhälle för att utforska nya tillämpningar. Än, lite är känt om de ultimata prestandabegränsningarna för Googles QAOA-algoritm.
Ett team av forskare från Skoltechs Deep Quantum Laboratory antog denna samtida utmaning. Hela Skoltech-teamet ledd av prof. Jacob Biamonte upptäckte och kvantifierade vad som verkar vara en grundläggande begränsning i det allmänt använda tillvägagångssätt som initierats av Google.
Rapporterar in Fysiska granskningsbrev , författarna beskriver upptäckten av så kallade nåbarhetsbrister – författarna visar att dessa brister sätter en grundläggande begränsning för QAOA:s förmåga att ens approximera en lösning på ett problem, exempel.
Skoltech-teamets resultat rapporterar en tydlig begränsning av den variationsmässiga QAOA-kvantalgoritmen. QAOA och andra variationsmässiga kvantalgoritmer har visat sig vara extremt svåra att analysera med hjälp av kända matematiska tekniker på grund av en intern kvant-till-klassisk återkopplingsprocess. Nämligen, en given kvantberäkning kan bara köras under en bestämd tid. Inom denna fasta tid, ett fast antal kvantoperationer kan utföras. QAOA strävar efter att använda dessa kvantoperationer iterativt genom att bilda en sekvens av allt mer optimala approximationer för att minimera en objektiv funktion. Studien sätter nya gränser för denna process.
Författarna upptäckte att QAOA:s förmåga att approximera optimala lösningar för alla kvantkretsar med fast djup är fundamentalt beroende av problemen "densitet". I fallet med problemet som kallas MAX-SAT, den så kallade densiteten kan definieras som förhållandet mellan problembegränsningarna och variabelt antal. Detta kallas ibland klausuldensitet.
Författarna upptäckte problematiska fall av hög densitet med optimala lösningar som inte kan approximeras med garanterad framgång, oavsett algoritmens körtid.