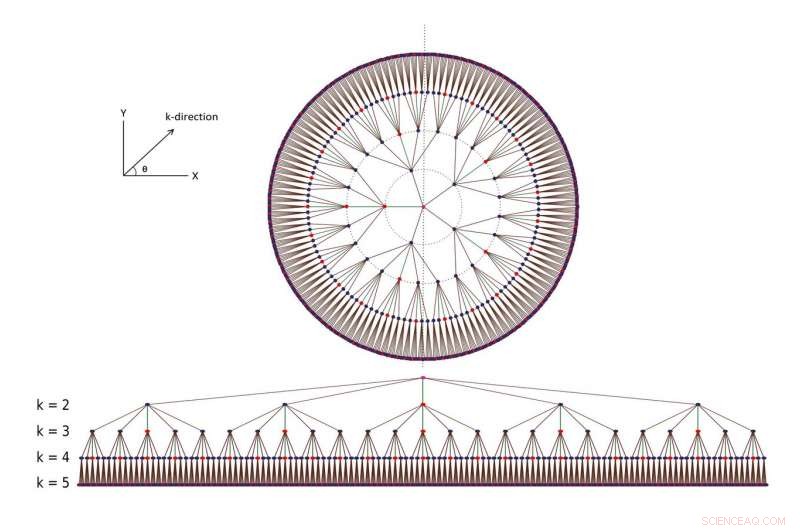
Kvantkretsen. Olika lager motsvarar olika feltoleranser, med det undre lagret som har den minsta feltoleransen. Kredit:Författare/Physical Review Letters
Kvantkretsar, byggstenarna i kvantdatorer, använda kvantmekaniska effekter för att utföra uppgifter. De är mycket snabbare och mer exakta än de klassiska kretsarna som finns i elektroniska enheter idag. I verkligheten, dock, ingen kvantkrets är helt felfri. Att maximera effektiviteten hos en kvantkrets är av stort intresse för forskare från hela världen.
Forskare vid Indian Institute of Science (IISc) har nu tagit itu med detta problem med hjälp av en matematisk analog. De tog fram en algoritm för att explicit räkna antalet datorresurser som behövs, och optimerade den för att få maximal effektivitet.
"Vi kunde [teoretiskt] bygga den mest effektiva kretsen och minska den mängd resurser som behövs av en enorm faktor, " säger Aninda Sinha, Docent vid Centrum för högenergifysik, IISc, och motsvarande författare till tidningen publicerad i Fysiska granskningsbrev . Forskarna föreslår också att detta är den högsta möjliga effektivitet som kan uppnås för en kvantkrets.
Att optimera kvantkretseffektiviteten är användbart inom olika områden, speciellt kvantberäkning. Inte bara kommer kvantdatorer att ge snabbare och mer exakta resultat än klassiska datorer, de kommer också att vara säkrare – de kan inte hackas, vilket gör dem användbara för skydd mot digitala bankbedrägerier, säkerhetsintrång och datastöld. De kan också användas för att hantera komplicerade uppgifter som att optimera transportproblem och simulera finansmarknaden.
Klassiska kretsar består av universella logiska grindar (som NAND- och NOR-grindar), som var och en utför fördefinierade operationer på ingången för att producera en utdata.
"Analogt, det finns universella kvantgrindar för att göra kvantkretsar. I verkligheten, grindarna är inte 100 procent effektiva; det finns alltid ett fel associerat med utgången från varje grind. Och det felet kan inte tas bort; det fortsätter helt enkelt att lägga till för varje grind som används i kretsen, "säger Pratik Nandy, Sinhas Ph.D. student och medförfattare till uppsatsen.
Den mest effektiva kretsen minimerar inte felet i utgången; snarare minimerar det de resurser som krävs för att få samma utdata. "Så frågan kokar ner till:givet en nettofeltolerans, vad är det minsta antalet grindar som behövs för att bygga en kvantkrets?" säger Nandy.
Under 2006, en studie ledd av Michael Nielsen, en före detta fakultetsmedlem vid University of Queensland, visade att att räkna antalet grindar för att uppnå maximal effektivitet motsvarar att hitta vägen med det kortaste avståndet mellan två punkter i något matematiskt utrymme med volym V. En separat studie från 2016 hävdade att detta antal borde variera direkt med V.
"Vi gick tillbaka till Nielsens ursprungliga verk och det visar sig att hans porträkning inte ger dig en variation med V, snarare varierar det med V 2 , " säger Sinha. Han och hans team generaliserade studiens antaganden och introducerade några modifieringar för att lösa optimeringsproblemet. "Våra beräkningar visade att det minsta antalet grindar verkligen varierar direkt med volymen, " han säger.
Förvånande, deras resultat verkar också koppla effektivitetsoptimeringsproblemet med strängteori, en berömd idé som försöker kombinera gravitation och kvantfysik för att förklara hur universum fungerar. Sinha och hans team tror att denna länk kan visa sig vara avgörande för att hjälpa forskare att tolka teorier som involverar gravitation. De syftar också till att utveckla metoder som beskriver en samling kvantkretsar för att beräkna vissa experimentstorheter som inte teoretiskt kan simuleras med befintliga metoder.