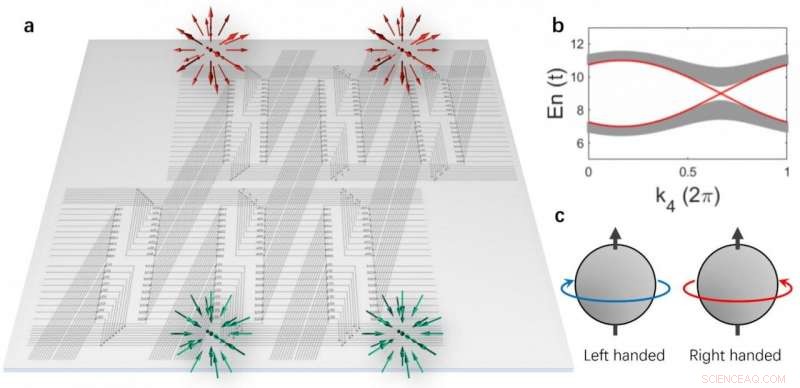
(a) 4D -kretsgitteret realiserat på ett 2D -plan. Ett par Weyl-punkter med samma kiralitet är lokaliserade på den tredimensionella gränsen. (b) Bulkbandstrukturerna och Weyl -gränsen (röda linjer). (c) Schematisk över Weyl -staternas kiralitet. Upphovsman:Science China Press
Under de senaste åren har topologi har framträtt som ett viktigt verktyg för att klassificera och karakterisera materialegenskaper. Det har visat sig att många material uppvisar ett antal ovanliga topologiska egenskaper, som inte påverkas av deformationer, t.ex., stretching, komprimering, eller vridning. Dessa topologiska egenskaper inkluderar kvantiserade hallströmmar, stor magnetoresistans, och yta excitationer som är immun mot störning. Man hoppas att dessa egenskaper kan användas för framtida teknik, Till exempel, elektronik med låg effekt, ultrasnabba detektorer, högeffektiva energiomvandlare, eller för kvantberäkning.
På senare tid, topologi har också tillämpats på syntetiska material, t.ex., fotoniska kristaller eller nätverk av elektriska kretsar. Dessa syntetiska material har flera fördelar jämfört med deras naturliga motsvarigheter. Till exempel, topologin för deras excitationer (dvs. deras excitationsband) kan kontrolleras och manipuleras exakt. Dessutom, på grund av deras långsiktiga gitteranslutning, syntetiska material kan realisera topologiska excitationer i dimensioner större än tre. Därav, syntetiska material, och i synnerhet elektriska kretsnät, erbjuder möjlighet att realisera ett antal intressanta topologiska egenskaper som inte är tillgängliga i verkliga material.
Rui Yu från Wuhan University, Yuxin Zhao från Nanjing University, och Andreas Schnyder från Max-Planck-institutet i Stuttgart har nu visat denna potential genom att uttryckligen konstruera ett elektriskt kretsnät som simulerar en fyrdimensionell (4-D) topologisk isolator med en klassisk tidsomvändningssymmetri [Fig. 1 (a)]. Topologiska isolatorer är material som isolerar i bulkvolymen, men mycket ledande vid ytan, på grund av gaplösa yta excitationer. Liknande, den simulerade 4-D topologiska isolatorn har ett excitationsgap i bulkvolymen, inom vilket det finns ett par ytaxcitationer [Fig. 1 (b)].
Dessa 3-D yta excitationer har en linjär dispersion, och mer intressant, de är av Weyl -typ med samma skicklighet, d.v.s. de har inre frihetsgrader som snurrar efter samma vänster- eller högerhänta regel med avseende på deras spridningsriktning [Fig. 1 (c)]. De har topologiskt ursprung och skiljer sig inte från någon ytaxcitation som finns i konventionella material. Topologi dikterar att dessa 3-D Weyl-excitationer måste komma i par och att de är robusta mot störningar och deformationer. Författarna har utfört detaljerade numeriska simuleringar av det topologiska kretsnätverket och har visat att 3D-Weyl-excitationerna lätt kan observeras i frekvensberoende mätningar.
Författarnas arbete visar att topologiska excitationer enkelt kan realiseras på kommersiellt tillgängliga kretskort eller integrerade kretsskivor som består av induktorer och kondensatorer. Det banar väg för att förverkliga godtyckliga typer av topologiska yta excitationer, till exempel, så kallade Dirac- eller Majorana-exciteringar av dimensioner två, tre, eller ännu högre. Elektrisk kretsimplementering av topologiska excitationer har fördelen av att vara enkel, lätt omkonfigurerbar, och tillåter en hög grad av kontroll. Detta kommer att göra det möjligt att studera i framtida topologiska fasövergångar, icke-linjära effekter, fenomen som inte är i jämvikt, och kvantöppna system (t.ex. icke-hermitiska system).