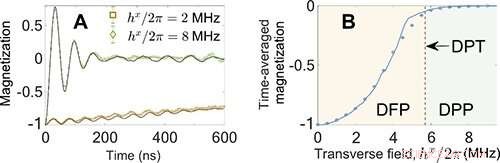
Fig. 1 Tidsutveckling av magnetiseringen och tidsgenomsnittad magnetisering som en funktion av tvärfältet. Kredit:IOP
Kvantsimulering använder ett kontrollerbart kvantsystem för att efterlikna komplexa system eller lösa svårlösta problem, bland vilka problem med icke-jämvikt i kvantsystem med många kroppar har väckt stort forskningsintresse. Sådana system är svåra att simulera med klassiska datorer. Istället, populära kvantsimulatorer, som supraledande kretsar, kan ge insikter i dessa problem. Eftersom avsevärda framsteg har gjorts i skalbarhet, koherens och kontrollerbarhet, supraledande kretsar har blivit en av de viktigaste kvantsimuleringsplattformarna.
Nyligen, en forskargrupp från Institute of Physics of the Chinese Academy of Sciences, Zhejiang University och RIKEN i Japan, har framgångsrikt utfört kvantsimulering av dynamiska fasövergångar i en Lipkin-Meshkov-Glick-modell med en 16-qubit supraledande kvantsimulator.
Dynamisk fasövergång (DPT) är en slags icke-jämviktsfasövergång och har teoretiskt undersökts i olika kvantmodeller för många kroppar. Det finns två typer av DPT. Den första typen (DPT-1) fokuserar på parametern för icke-jämviktsordning, medan den andra typen (DPT-2) kännetecknas av det icke-analytiska beteendet hos Loschmidt-ekot associerat med Lee-Yang-Fishers nollor i statistisk mekanik. Ytterligare teoretiska och numeriska undersökningar har visat att DPT-1 och DPT-2 kan studeras i samma ramverk.
Kvantprocessorn integrerar 20 supraledande qubits, alla kopplade till en gemensam resonatorbuss, som användes för att generera Schrödinger-katttillstånd i tidigare arbete. Den här gången, 16 qubits användes för att konstruera Lipkin-Meshkov-Glick (LMG)-modellen genom att applicera kontrollerbart tvärfält på varje qubit. Systemet drivs in i ett icke-jämviktstillstånd med mikrovågor och utvecklas sedan under LMG-modellen.
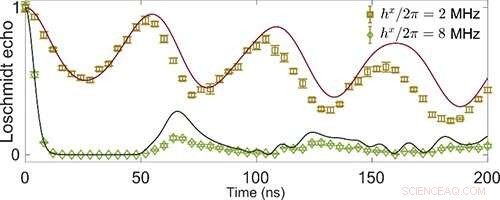
Fig. 2 Tidsutveckling av Loschmidt-ekot. Upphovsman:IOP
Forskarna observerade först typiska egenskaper hos DPT-1. För det lilla tvärfältet, systemet förblir i den dynamiska ferromagnetiska fasen (DFP), och magnetiseringen uppvisar en långsam avslappning. Dock, givet ett starkt tvärfält, systemet går in i den dynamiska paramagnetiska fasen (DPP), där magnetiseringen uppvisar en stor oscillation vid en tidig tidpunkt och närmar sig noll i långtidsgränsen. Den tidsgenomsnittliga magnetiseringen som parameter för icke-jämviktsordning är noll i DPP, medan det blir ändligt i DFP.
Sedan demonstrerade de förekomsten av Loschmidt-ekots nollor i DPP, antyder förhållandet mellan DPT-1 och DPT-2. Dessutom, forskarna utforskade DPT från ett nytt perspektiv. De studerade minsta spinnklämning som en sond för fasövergången.
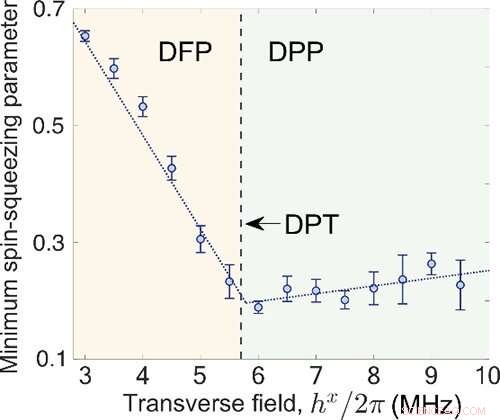
Fig. 3 Den minsta spin-squeezing-parametern som funktion av tvärfältet. Kredit:IOP
De experimentella resultaten visar att minimivärdet för spin-squeezing-parametrarna kan uppnås mycket nära den kritiska punkten för DPT. Detta indikerar en potentiell tillämpning av DPT på kvantmetrologi.
Den här studien, med titeln "Söka dynamiska fasövergångar med en supraledande kvantsimulator, "publicerades i Vetenskapliga framsteg .