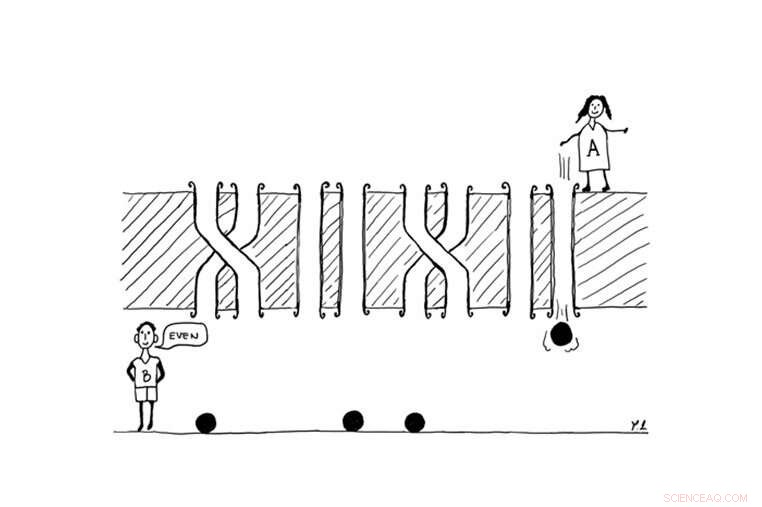
Figuren visar det enklaste exemplet på paritetsspel. Alice (A) slår ett visst antal kulor mot Bob (B), i syfte att lära sig om antalet tvinnade rör är jämnt eller udda. Spelarna behöver fyra vanliga klassiska kulor för att klara uppgiften. I kontrast, redan två kvantmarmor skulle räcka. Upphovsman:© Borivoje Dakić
Som Richard Feynman berömt uttryckte det, "dubbelspaltsexperimentet är absolut omöjligt att förklara på något klassiskt sätt och har i det kvantmekanikens hjärta. I verkligheten, den innehåller det enda mysteriet. "
Verkligen, i detta experiment, en kvantpartikel beter sig som om den befann sig på två olika platser samtidigt, och uppvisar paradigmatiska vågliknande fenomen som störningar. Dock, det noterades senare att experiment med flera slitsar visar att graden av delokalisering av kvantpartiklar har sina gränser, och det i viss mening, kvantpartiklar kan inte samtidigt delokaliseras på mer än två platser. Denna begränsning har skapat ett pussel som än idag inte har lösts helt. Forskare vid universitetet i Wien och IQOQI-Wien (österrikiska vetenskapsakademin) har tagit ett betydande steg mot att förstå detta problem genom att omformulera interferensförsök när det gäller informationsteoretiska spel. Deras analys, som nyligen har dykt upp i tidskriften Quantum, ger ett intuitivt sätt att tänka på störningsfenomen och dess begränsningar, därigenom banar vägen för att lösa det ovannämnda pusslet.
En av de mest slående särdragen i kvantmekaniken är superpositionsprincipen. Denna princip kan lättast illustreras via dubbelspaltsexperimentet, som involverar en partikel som skickas genom en platta genomborrad med två slitsar. Enligt våra vanliga vardagliga intuitioner, man kan förvänta sig att partikeln alltid passerar antingen genom en slits, eller genom den andra. Dock, kvantmekanik innebär att partikeln i viss mening kan passera genom båda slitsarna samtidigt, det är, det kan vara i en superposition av två platser samtidigt. Denna möjlighet ligger till grund för fenomenet kvantinterferens, dvs det slående vågliknande beteendet som uppvisas av kvantpartiklar. Nu, finns det ett sätt att kvantifiera i vilken grad kvantpartiklar kan avlokaliseras? Tillåter kvantteori partiklar att korsa mer än två vägar samtidigt? För att förstå dessa frågor, fysiker har analyserat "experiment med flera slitsar, ", som skiljer sig från dubbelspaltsexperimentet endast i antalet slitsar:till exempel ett trippel-slits experiment innefattar en partikel som skickas genom tre slitsar.
Man kan tro att om en kvantpartikel kan passera genom två slitsar samtidigt, det bör också kunna passera genom tre samtidigt, fyra, eller valfritt antal slitsar. Förvånande, det noterades omedelbart att alla mönster som erhållits i flerslitsförsök kan förklaras av att partikeln alltid passerar högst två slitsar samtidigt. Även om den här funktionen är matematiskt till fullo förstått, följande frågor förblir obesvarade:finns det en fysisk orsak till den uppenbara asymmetrin mellan experiment med dubbelslits och experiment med flerslits? Vad ligger till grund för denna något godtyckliga begränsning av "delokalisering" av kvantpartiklar?
I deras senaste arbete, Sebastian Horvat och Borivoje Dakić, forskare vid universitetet i Wien och IQOQI-Wien (österrikiska vetenskapsakademin), har tagit ett betydande steg mot att förstå detta problem genom att ta itu med det med informationsteori. Nämligen, de har omformulerat störningsfenomen och experiment med flera slitsar när det gäller "paritetsspel", det enklaste exemplet illustreras i figuren. Spelet omfattar två spelare, Alice och Bob, som separeras av en vägg genomborrad med fyra par rör. Varje par rör kan antingen vara raka eller vridna, och antalet tvinnade par är okänt både för Alice och för Bob. Vidare, Alice förfogar över ett visst antal kulor som hon kan flicka genom rören mot Bob; spelarna kan använda dessa kulor för att lära sig något om rörens struktur.
Målet med spelet är att spelarna ska samarbeta och ta reda på om det totala antalet tvinnade par är jämnt eller udda, genom att använda det minsta möjliga antalet kulor. Nu, anta att Alice kastar en marmor genom ett av rören, till exempel genom den andra. Bob kan sedan enkelt utläsa om det första paret av rör är rakt eller vridet genom att helt enkelt kontrollera om marmorn har fallit genom det andra röret eller genom det första. Analogt, om Alice har fyra kulor till förfogande, hon kan flicka var och en av dem genom det högra röret i varje par (som det är fallet i figuren). Bob kan sedan rakt utleda antalet tvinnade par, och alltså om detta tal är jämnt eller udda, och därmed vinna spelet. Dock, om antalet rörpar överstiger antalet kulor som Alice har till förfogande, då kan spelet inte vinnas, eftersom det alltid kommer att finnas minst ett rörpar, om vilken Bob inte kan samla någon som helst information. Därför, för att vinna spelet, spelarna måste använda lika många kulor som det finns par rör.
Å andra sidan, kvantmekanik, och mer specifikt, överlagringsprincipen, gör det möjligt för spelarna att vinna spelet som illustreras i figuren genom att bara använda två "kvantmarmor"! Ett sätt att förstå var denna förbättring kommer ifrån är att komma ihåg, som det nämnts tidigare, att en kvantpartikel kan "passera genom två platser samtidigt". Två kvantmarmor kan således "samtidigt passera genom fyra platser", därmed efterliknar beteendet hos fyra vanliga (klassiska) marmor. "I det här spelet, kulor uppträder analogt med tokens som kan sättas in genom rören. När Alice sätter in en vanlig klassisk marmor, det är som om hon satte in 1 öre.
Å andra sidan, som kvantteori tillåter kulor att "passera genom två rör samtidigt", varje kvantmarmor är värd 2 slantar. Värdet på tokens är additivt:till exempel för att vinna spelet, Alice kan antingen sätta in 4 klassiska kulor eller 2 kvantmarmor, eftersom det totala tokenvärdet i båda fallen är lika med 4 öre ", förklarar Sebastian Horvat. Å andra sidan, kom ihåg att en kvantpartikel inte kan passera genom mer än två platser samtidigt:detta återspeglas i det faktum att Alice och Bob inte kan vinna spelet genom att använda mindre än två kvantmarmor. Därav, för att vinna spelet, antalet kvantmarmor som skickas av Alice måste vara lika med minst hälften av det totala antalet rörpar.
I deras arbete, forskarna har analyserat mer allmänna formuleringar av detta spel och har studerat spelarnas prestanda beroende på antalet partiklar och om partiklarna är klassiska, kvant, eller av mer allmänna och hypotetiska slag. Borivoje Dakić tillägger:"Dessa hypotetiska partiklar har högre informationsteknik, det är, deras motsvarande tokens är giltiga mer än 2 slantar. Det är inte klart varför naturen ska föredra klassiska och kvantpartiklar framför dessa hypotetiska:detta är något som vi fortfarande måste studera i framtiden. "
Allt som allt, paritetsspel ger en alternativ beskrivning av kvantstörningar inom en mer allmän och intuitiv ram, som förhoppningsvis kommer att belysa nya funktioner i kvantöverlagring, på samma sätt som hur studiet av kvantinvikling har fördjupats genom formuleringen av de så kallade "icke-lokala spelen".