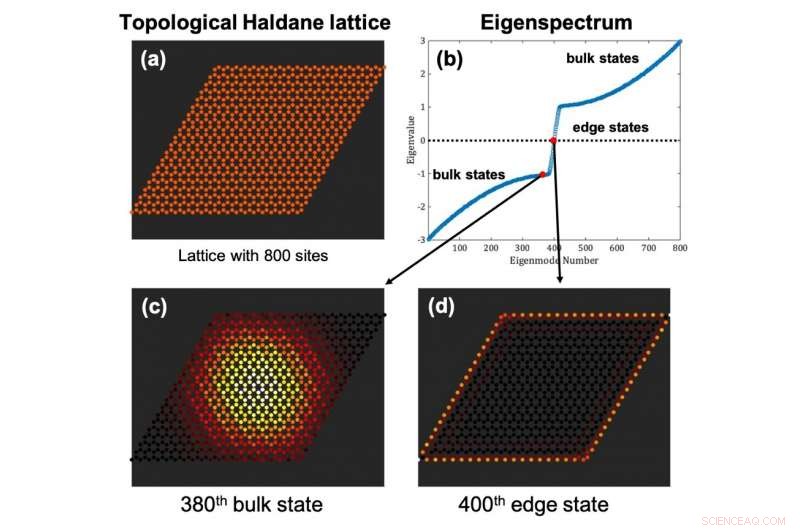
Figur 1:Topologiska isolatorer är finitstora gittersystem (a) som uppvisar eigenspectra där (b) egenenergier från bulktillstånd (c) uppvisar ett bandgap som (d) innehåller egenenergier från så kallade kanttillstånd. Kredit:MBI/HU
I en gemensam insats, forskare från Humboldt-Universität (Berlin), Max Born Institute (Berlin) och University of Central Florida (USA) har avslöjat de nödvändiga förutsättningarna för robust transport av intrasslade tillstånd av tvåfotonljus i fotoniska topologiska isolatorer, banar väg mot bullerbeständig transport av kvantinformation. Resultaten har dykt upp i Naturkommunikation.
Ursprungligen upptäckt i system för kondenserade ämnen, topologiska isolatorer är tvådimensionella material som stöder spridningsfri (enkelriktad) transport längs sina kanter, även i närvaro av defekter och störningar. I huvudsak, topologiska isolatorer är finita gittersystem där, givet en lämplig avslutning av det underliggande oändliga gittret, kanttillstånd bildas som ligger i ett väldefinierat energigap associerat med bulktillstånden, dvs dessa kanttillstånd är energetiskt separerade från bulktillstånden (fig. 1).
Viktigt, enpartikelkanttillstånd i sådana system är topologiskt skyddade från spridning:De kan inte spridas in i bulken på grund av att deras energi ligger i gapet, och de kan inte spridas bakåt eftersom bakåtriktade kanttillstånd antingen saknas eller inte är kopplade till de framåtriktade kanttillstånden.
Möjligheten att konstruera komplexa Hamiltonianer med hjälp av integrerade fotoniska gitter i kombination med tillgången på intrasslade fotoner höjer den spännande möjligheten att använda topologiskt skyddade intrasslade tillstånd i optisk kvantberäkning och informationsbehandling (Science 362, 568, (2018), Optica 6, 955 (2019)).
För att uppnå detta mål, dock, är mycket icke-trivialt, eftersom topologiskt skydd inte helt sträcker sig till spridning av flera partiklar (rygg). I början, detta faktum verkar vara kontraintuitivt eftersom individuellt, varje partikel skyddas av topologi, samtidigt som intrasslade (korrelerade) partiklar blir mycket mottagliga för störningar av det ideala gittret. Den underliggande fysiska principen bakom denna uppenbara diskrepans är att, kvantmekaniskt, identiska partiklar beskrivs av tillstånd som uppfyller en utbytessymmetriprincip.
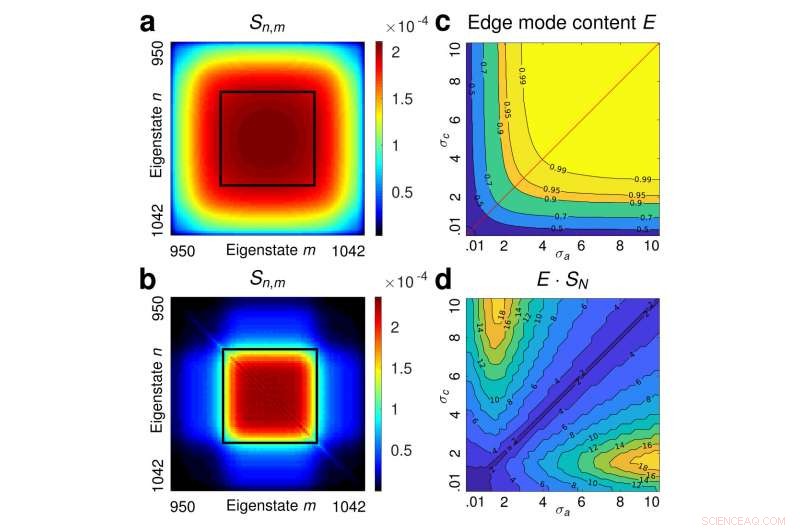
Figur 2:För att identifiera det topologiska skyddsfönstret, forskarna betraktade ett spektralt brett produkttillstånd som initialtillstånd och förökade det genom en ensemble av 1000 slumpmässiga Haldane -galler. (a) Visar den spektrala korrelationskartan för det initiala tillståndet och i (b) visas ensemble-genomsnittet av de spektrala korrelationskartorna inuti kantkantsunderrummet efter utbredningen genom ensemblen av oordnade gitter. Det har visat sig att de enda två-fotonamplituderna som överlever spridningen som induceras av störningen ligger i området som indikeras av den svarta fyrkanten som är skyddsfönstret. Till sist, (c) och (d) display, respektive, kantmodsinnehållet E och produkten av kantmodsinnehållet med Schmidt-numret E · SN som en funktion av varianserna för initialtillstånden. Kredit:MBI/HU
I deras arbete, forskarna gör flera grundläggande framsteg mot att förstå och kontrollera topologiskt skydd i samband med multipartikeltillstånd:
Att vara precis, de utforskar störningens inverkan på en rad tvåfotontillstånd som sträcker sig från de fullt korrelerade till de helt antikorrelerade gränserna, därigenom också täcka ett helt separerbart tillstånd. För deras analys, de överväger två topologiska galler, en periodisk och en aperiodisk. I det periodiska fallet, de anser Haldane-modellen, och för det aperiodiska fallet, ett kvadratiskt galler, vars enpartikeldynamik motsvarar kvanthalleffekten, studeras.
Resultaten erbjuder en tydlig färdplan för att generera robusta vågpaket som är skräddarsydda för den speciella störningen. Specifikt, de fastställer gränser för stabiliteten hos intrasslade tillstånd upp till relativt höga grader av intrassling som erbjuder praktiska riktlinjer för att generera användbara intrasslade tillstånd i topologiska fotoniska system. Ytterligare, dessa fynd visar att för att maximera intrassling utan att offra topologiskt skydd, den gemensamma spektralkorrelationskartan över tvåfotontillstånd måste passa in i ett väldefinierat topologiskt skyddsfönster. (Fig. 2).