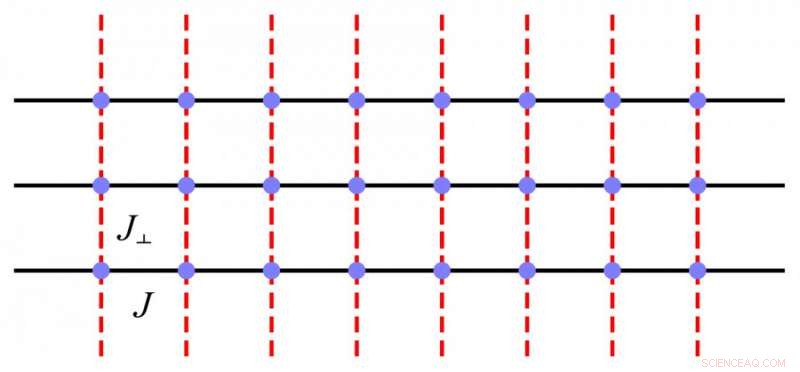
Diagram 1. Kopplade spinn-kedjor med närmaste-granne spin-intrakedjeinteraktion (heldragen svart linje) och interkedjeinteraktion (röd streckad linje). Kredit:University of Hong Kong
Under 2013, François Englert och Peter Higgs vann Nobelpriset i fysik för den teoretiska upptäckten av en mekanism som bidrar till vår förståelse av ursprunget till massan av subatomära partiklar, vilket bekräftades genom upptäckten av den förutspådda fundamentala partikeln av A Toroidal LHC Apparatus (ATLAS) och Compact Muon Solenoid (CMS) experiment vid European Organization for Nuclear Research (CERN) Large Hadron Collider 2012. Higgs-läget eller Anderson-Higgs-mekanismen (uppkallad efter en annan Nobelpristagare Philip W Anderson), har ett utbrett inflytande i vår nuvarande förståelse av den fysiska lagen för massa som sträcker sig från partikelfysik - den svårfångade "Gudspartikel" som Higgs boson upptäckte 2012 till de mer välbekanta och viktiga fenomenen superledare och magneter inom kondensmaterialfysik och kvantmaterialforskning.
Higgs-läget, tillsammans med Goldstone-läget, orsakas av det spontana brytandet av kontinuerliga symmetrier i de olika kvantmaterialsystemen. Dock, skiljer sig från Goldstone-läget, som i stor utsträckning har observerats via neutronspridning och kärnmagnetisk resonansspektroskopi i kvantmagneter eller supraledare, observationen av Higgs -läget i materialet är mycket mer utmanande på grund av dess vanliga överdämpning, som också är egenskapen i partikelfysikens kusin - den svårfångade Higgs -bosonen. För att försvaga dessa dämpningar, två vägar har föreslagits från den teoretiska sidan, genom (1) kvantkritiska punkter och (2) dimensionell övergång från höga dimensioner till lägre. För (1), människor har uppnått flera anmärkningsvärda resultat, Det finns få framgångar i (2).
För att uppfylla denna kunskapslucka, från 2020, Herr Chengkang Zhou, sedan en förstaårs Ph.D. studerande, Dr Zheng Yan och Dr Zi Yang Meng från forskningsavdelningen för fysik och astronomi vid University of Hong Kong (HKU), designade en dimensionell crossover-inställning via kopplade spinnkedjor. De tillämpade quantum Monte Carlo (QMC) simulering för att undersöka excitationsspektra för problemet. Samarbetar med Dr. Hanqing Wu från Sun Yat-Sen University, Professor Kai Sun från University of Michigan, och professor Oleg A Starykh från University of Utah, de observerade tre olika typer av kollektiv excitation i kvasi-1D-gränsen, inklusive Goldstone-läget, Higgs-läget och det skalära läget. Genom att kombinera numeriska och analytiska analyser, de förklarade framgångsrikt dessa excitationer, och i synnerhet, avslöjade den tydliga närvaron av Higgs-läget i de kvasi-1D kvantmagnetiska systemen. Alla dessa resultat kan inte bara hjälpa till att hitta de viktigaste modellparametrarna för materialet, men avslöjar också en bild av hur dimensionen spelar roll i det kondenserade materialet. Dessa forskningsrön publiceras i Fysiska granskningsbrev .
Bakgrund
Kvantmaterial är inbäddade i vårt dagliga liv, såsom olika elektroniska komponenter, datorchip, och solpaneler. Med den snabba utvecklingen av vetenskap och teknik, förståelsen och manipulationen av de kvantmånga kroppsinteraktionerna i materialen spelar en allt viktigare roll. En sådan tendens har redan visat sitt första tecken. Till exempel, 2D quantum moiré-materialen, som den magiska vinkeln vriden dubbelskiktsgrafen, har rönt stor uppmärksamhet och visar sin nya prestation när det gäller att realisera supraledning i kolbaserade istället för de traditionella kiselbaserade materialen. Dessutom, kvantdatorteknik, som bygger på teorin om supraledning och till och med topologi utvecklas snabbt för att bygga mer effektiva datorchips bortom Moores lag. Tillsammans med dessa ansträngningar, forskningen om kvantmagneter är ett av de viktigaste objekten, där detekteringen av Higgs-läget och Goldstone-lägena kan avslöja de underliggande modellparametrarna för materialet.
Dock, eftersom växelverkan mellan miljarder elektroner måste beaktas, det är svårt att peka ut en tydlig bild av flera kvantmånga kroppssystem via kvantmekanik direkt. Därför, numeriska metoder, såsom QMC-simuleringen, har blivit användbara tekniker för att studera kvantsystem för många kroppar. Dessa numeriska metoder kan berätta användbar information och egenskaper hos kvantmångkroppssystem och visa mikromekanismen hos dessa system. Denna information skulle stimulera utvecklingen av teorin samt vägleda den experimentella designen, vilket skulle hjälpa forskare och ingenjörer att ta reda på mer nya kvantmaterial och komponenter.
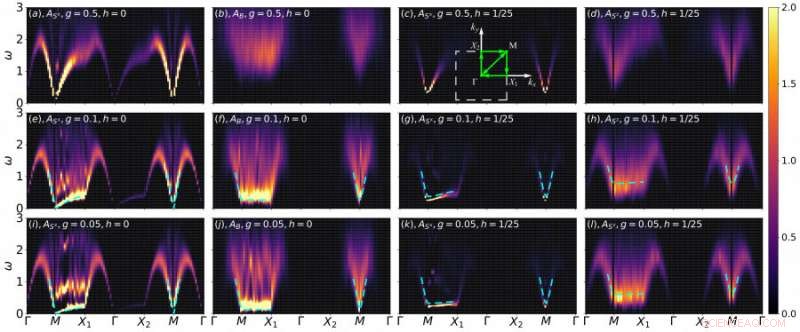
Diagram 2. Spektra för Goldstone-läget, Higgs-läget, och det skalära läget ändras med de kopplade spinnkedjorna som tenderar till en kvasi-1D-gräns. Den första och den tredje kolumnen är för Goldstone-läget. Den andra talar om det skalära läget medan det fjärde är Higgs-läget. Kredit:University of Hong Kong
Higgs -läget via dimensionell crossover
För att studera mikromekanismen i kvantmångkroppssystem, numeriska fysiker brukar komma med en enkel modell baserad på teoretisk förståelse och experimentella data. Sedan, de tillämpar numeriska simuleringsmetoder för att studera modellen i en region med rimliga parametrar. Ett sådant forskningsförfarande har använts i undersökningen av Higgs-läget i kvantmagneterna, ändå är dess observation fortfarande utmanande på grund av dess vanliga överdämpningsfunktion. Från den kvantteoretiska sidan, forskare har föreslagit två vägar. Den första är genom den kvantkritiska punkten. På denna väg, det finns flera anmärkningsvärda resultat, inklusive signalen från Higgs -läget har observerats i C 9 H 18 N 2 CuBr 4 . Men den andra vägen, som går genom den dimensionella korsningen mot 1D, är fortfarande full av tomt och kräver mer studier, dels för att det är svårt att hitta ett kvantmångkroppssystem med dimensionsreduktion. En sådan dimensionsreduktion försvagar systemets långväga ordning och, därför, hämmar överdämpningsfunktionen i Higgs -läget. Forskargruppen från University of Hong Kong, Sun Yat-Sen University, University of Michigan och University of Utah lyckades uppfylla dessa ämnen genom att numeriskt simulera en dimensionell crossover-kvantspinnmodell, kopplade spinnkedjor (se diagram 1).
Forskargruppen kom fram till en modell för kopplade spinnkedjor genom att introducera interkedjeinteraktionen. Genom att minska styrkan hos dessa interkedjiga interaktioner (ändra värdet på J⊥ i figur 1 mot 0), modellen skulle förändras från ett 2D-system till ett kvasi-1D-system. Forskargruppen använde QMC-metoden som simulerade modellen och utvecklade en effektiv metod för att mäta spin- och obligationskorrelationsfunktionerna. De observerade inte bara Higgs-läget via en dimensionell korsning utan hittar också det skalära läget, vilket förutsägs av sinus-Gordon-teorin. Dessa resultat gör kopplade spinnkedjor till ett attraktivt kandidatsystem för att studera kollektiv kvantdynamik teoretiskt och experimentellt.
Higgs-läget och det skalära lägesspektrumet
Med hjälp av superdatorerna Tianhe-II och III, forskargruppen studerade de kopplade spinnkedjorna i kvasi-1D-gränsen och observerade utvecklingen av spektret av Goldstone-läge (figur 2 (g) och (k)), Higgs-läget (diagram 2 (h) och (l)), och det skalära läget (Figur 2 (f) och (j)). Figur 2 visar de erhållna spektra från QMC -simuleringarna, där den blå streckade linjen representerar spridningsrelationen enligt kombinationen av medelfältsteorin och sin-Gordon teorimodellen. Som man kan se i figur 2, de numeriska resultaten stämmer väl överens med teoriförutsägelsen, vilket innebär att forskargruppen har lyckats fånga signalen från Higgs-läget. Dessa signaler är mycket användbara för att utforma motsvarande experiment för att observera Higgs-läget via en dimensionell korsning, som neutronspridning och kärnmagnetisk resonansspektroskopi. Sådana spännande resultat kommer också att bidra till vår förståelse av Higgs -läget i dimensionsreduktion.
För att beskriva uppkomsten av Higgs-läget och det skalära läget, forskargruppen ritade också ut frekvensberoendet för dem (se diagram 3), där g är en faktor som talar om hur nära modellen till kvasi-1D är. När g=1, de kopplade spinnkedjorna är i ett 2D-system, och med g =0, de kopplade spinnkedjorna finns i ett 1D -system. Genom att jämföra spektrumets frekvensberoende med olika g, man kan hitta en skarp topp som dyker upp när g minskar, vilket betyder att signalerna från Higgs-läget och det skalära läget blir starkare och starkare.
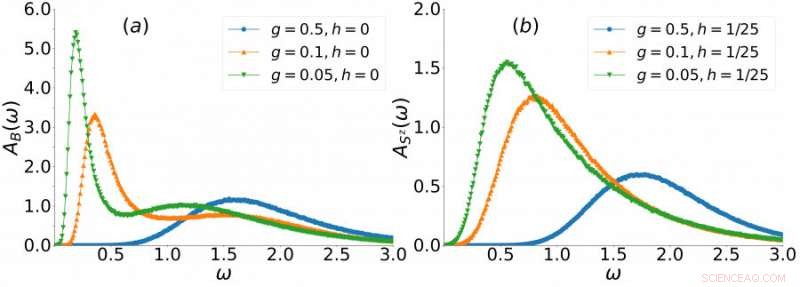
Diagram 3. Frekvensberoendet för spektrumet för Higgs-moden (b) och den skalära moden (a) utvecklas med dimensionsreduktionen. I denna dimensionsreduktion, en skarp topp växer fram, vilket innebär att signalen från det skalära läget och Higgs-läget blir starkare. Kredit:University of Hong Kong
Det nya fysikfenomenet via dimensionell korsning
Inom ramen för modern fysik, symmetri och dimension är två av de viktigaste faktorerna som bestämmer egenskaperna hos kvantmångkroppsfysiken. Och fenomenet som orsakas av dimensionsreduktion är ett nyckelämne i kvantmagnetiska system. Resultatet av forskargruppen gav en attraktiv modell och datastöd, som hjälper oss att förstå vilken väsentlig roll dimensionen spelar i vår värld och stimulerar utvecklingen av nästa generations kvantmaterial och komponenter.