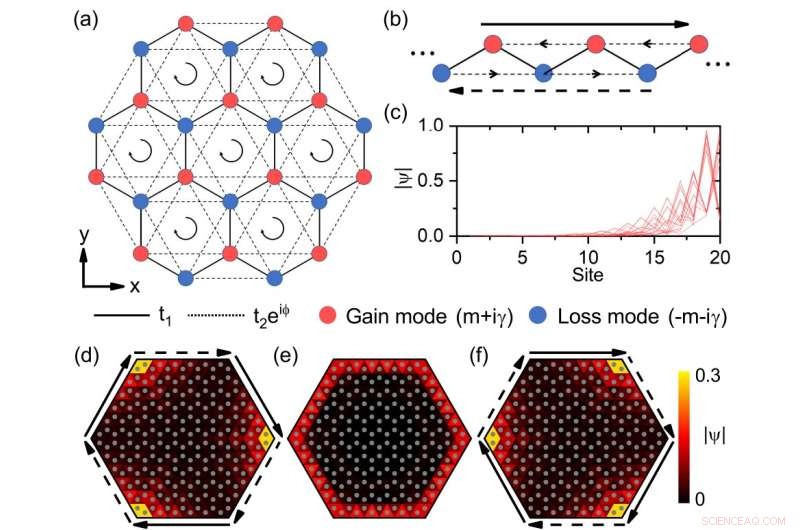
Fig. 1 Hybrid hudtopologiska lägen i icke-Hermitian Haldane-modell. (a) Schematisk över det icke-hermitiska gittret. De röda (blå) cirklarna anger platser med motsatta massatermer på plats +(m+iγ). (b) Sicksackkant av bikakegittret som en 1D-kedja, som har icke-hermitisk hudeffekt med vinst och förlust på plats. Den långa heldragna (streckade) pilen indikerar den kirala kantströmmen längs (motsatt) den lokaliserade riktningen [liknande i (d) och (f)]. De svarta pilarna i (a) och mittlinjepilarna i (b) indikerar riktningarna för kopplingarna närmast närmaste granne t2 e iφ . (c) Profil för alla egenmoder för 1D-kedjan i (b) med 20 platser. Vinsten och förlusten på plats är γ=3. (d)-(f) Den kirala kantmoden för γ=0 (e) blir hudtopologiska moder för γ=-0,6 (d) och γ=0,6 (f) med olika lokaliserade riktningar. Varje triangel med en grå cirkel anger en plats. Här fortplantar sig det kirala kantläget medurs. Kredit:Tsinghua University
Nyligen har docent Yong-Chun Liu vid institutionen för fysik och andra funnit den hybrida hudtopologiska effekten som induceras av vinst och förlust och paritets-tidsfasövergången mellan hudtopologiska lägen. Forskningsresultaten publicerades i Physical Review Letters under titeln "Gain-loss-induced hybrid skin-topological effect."
Icke-hermitiska system är öppna system som kan beskrivas av icke-hermitiska Hamiltonianer. Det finns många nya egenskaper i icke-hermitiska system, varav en är den icke-hermitiska hudeffekten. I denna effekt är alla egentillstånd för ett topologiskt system (inklusive bulktillstånd och kanttillstånd) lokaliserade till en av systemgränserna, och den konventionella bulkkantkorrespondensen bryts ner. Det finns huvudsakligen två sätt att realisera icke-hermitiska system:ett är att använda icke-reciproka kopplingar och det andra är att använda vinst och förlust.
I fallet med icke-reciproka kopplingar kommer icke-hermiticiteten från den icke-hermitiska karaktären av interaktionen mellan olika gitterplatser. Energiutbytet mellan gitterplatserna är asymmetriskt, så det blir ett nettoenergiflöde i en riktning och all energi samlas slutligen på gränsen. Således uppvisar de icke-ömsesidiga systemen hudeffekten. I fallet med förstärkning-förlust, härrör icke-hermiticiteten från förstärkningen och förlusten vid varje gitterplats, vilket är ekvivalent med att lägga till imaginär energi på plats till varje gitterplats. Denna typ av icke-hermitiskt system leder inte alltid till hudeffekten. I realistiska system är icke-reciproka kopplingar vanligtvis svåra att uppnå, men förlusten är utbredd, och förskjuten förlustfördelning är ekvivalent med vinst och förlust. Därför är det av stor betydelse att studera hudeffekten i system som inte är hermitiska med vinstförlust.
De fann den hybridhudtopologiska effekten inducerad av vinst och förlust i tvådimensionella system. Denna typ av hudeffekt är selektiv, dvs. bulktillstånden och kanttillstånden har olika beteende. Bulktillstånden påverkas inte av hudeffekten och förblir utsträckta, medan kanttillstånden uppvisar hudeffekt och är ytterligare lokaliserade till hörn. Detta hybridfenomen av hudeffekt och topologisk effekt visar de unika egenskaperna hos icke-hermitiska topologiska system, som inte har hermitiska eller icke-topologiska analoger.
Som ett specifikt exempel betraktade de den icke-hermitiska Haldane-modellen med vinst och förlust [Fig. 1 (a)]. I Haldane-modellen erhålls de topologiska kanttillstånden genom att introducera energi på plats och lokalt magnetiskt flöde. Det är en av de två viktiga modellerna för att förverkliga den kvantanomala Hall-effekten i den kondenserade materiens fysik. De fann att om förskjuten vinst och förlust introduceras i de närmaste grannplatserna i Haldane-modellen, kommer systemets topologiska kantlägen att uppvisa hudeffekten och är lokaliserade till hörnen, medan bulklägena inte påverkas. Så det avslöjar en hybrid hudtopologisk effekt.
Genom att enbart analysera gitterställena vid kanterna kan denna andra ordningens hudtopologiska effekt förenklas till första ordningens hudeffekt vid kanterna. I den förenklade endimensionella modellen finns det kirala kantströmmar på grund av det icke-lokala magnetiska flödet som introduceras av de komplexa kopplingarna närmast närmaste granne. De är ekvivalenta med icke-reciproka kopplingar, så systemet uppvisar den första ordningens hudeffekt [Fig. 1 (b)—(c)]. Tvärtom, det finns bara lokalt flöde, och icke-ömsesidigheten upphör i huvuddelen av systemet. Så bulklägena påverkas inte av hudeffekten. Genom att justera systemets förstärkning och förlust kan kantströmmarnas riktning ändras för att styra riktningen för den hudtopologiska effekten [Fig. 1 (d)—(f)].
De erhöll vidare förhållandet mellan paritetstid (PT) symmetrierna i systemet och den hybrida hudtopologiska effekten. När man väljer det öppna gränsvillkoret och det periodiska gränsvillkoret i olika riktningar, uppvisar systemet olika typer av PT-symmetrier för olika sorters kanter. Den globala PT-symmetrin som kartlägger vilket läge som helst lokaliserat i en gräns till den andra gränsen utesluter uppkomsten av den hybrida hudtopologiska effekten, medan den lokala PT-symmetrin med kartläggning inuti varje subcell tillåter existensen av den hybridhudtopologiska effekten.
Därför ger analysen av PT-symmetrier i systemet ett enkelt och effektivt sätt att bedöma om det finns den hybrida hudtopologiska effekten. I synnerhet fann de att när vinsten och förlusten i systemet ökar, kommer PT-fasövergången att ske mellan hudtopologiska lägen, åtföljd av uppkomsten av exceptionella punkter (EP). När PT-symmetri bryts är egenenergierna för de hudtopologiska moderna inte längre reella och fördelningarna av motsvarande egenmoder blir PT-asymmetriska.
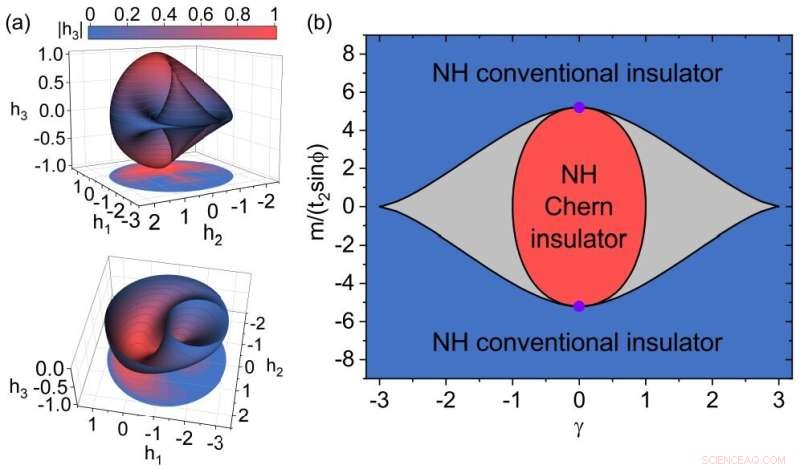
Fig. 2 The topology and phase diagram of the non-Hermitian Haldane model. (a) The surface S mapped from the first Brillouin zone, i.e., mapping from (kx , ky ) to (h1 , h2 , h3 ). The color map represents the magnitude of h3 . The density map below is the projection of the surface. The bottom figure is half of the top figure for h3 <0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points. Credit:Tsinghua University
In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.
The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics. + Utforska vidare