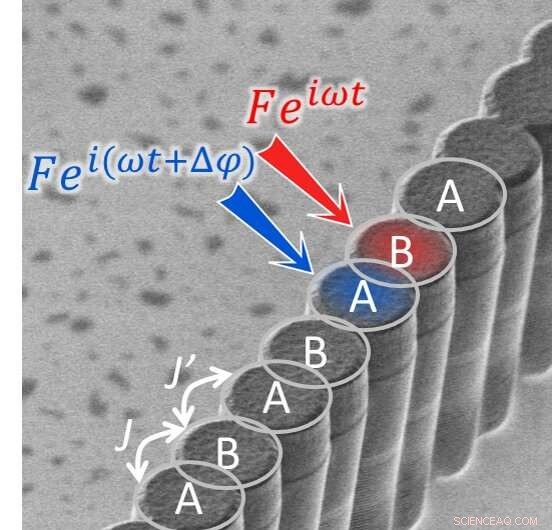
Svepelektronmikroskopibild som visar en kedja av halvledarkaviteter. Avståndet mellan kaviteterna är modulerat, vilket ger upphov till två olika värden på kopplingen J och J’ mellan intilliggande kaviteter (representerade schematiskt med dubbla vita pilar). Denna modulering av kopplingen ger gittret topologiska egenskaper. Två kaviteter i gittret exciteras av två lasrar med amplitud F, vinkelfrekvens och uppvisar en fasskillnad. Kredit:C2N/CNRS.
Topologisk fotonik är ett snabbt utvecklande forskningsområde som fokuserar på design av fotoniska gitter där ljusets beteende är inspirerat av topologiska isolatorers fysik. Medan de flesta studier inom detta område presenterade fotoniska system med linjära topologiska egenskaper, har nya arbeten börjat lägga grunden för icke-linjär topologisk fotonik.
Forskare vid Université Paris-Saclay CNRS har nyligen rapporterat det olinjära svaret från ett topologiskt gitter som implementerar en driven-dissipativ version av Su-Schrieffer-Heeger-modellen; en berömd elementär topologisk ram som beskriver partiklar som hoppar på ett 1D-gitter. Resultaten som samlats in av teamet vid Université Paris-Saclay CNRS, publicerade i Nature Physics , visar att koherent drivning i topologiska gitter kan utnyttjas, vilket gör det möjligt för fysiker att stabilisera nya olinjära faser.
"Under 2017 demonstrerade vår grupp den första topologiska lasern med ett 1D-gitter av halvledarresonator som mycket liknar den som användes i vår senaste studie," berättade Sylvain Ravets och Jacqueline Bloch, två av forskarna som utförde studien, till Phys.org . "I detta tidiga arbete använde vi dock systemets linjära topologiska egenskaper."
Den nyligen gjorda studien av Ravets, Bloch och deras kollegor bygger på deras tidigare forskningsansträngningar, i syfte att utvidga deras undersökning till icke-linjär topologisk fysik, som hittills huvudsakligen har utforskats inom ramen för konservativa system. I sina experiment använde forskarna en plattform med en betydande optisk olinjäritet, som utsätts för kontinuerlig drivning och förlust.
"Vi använde nanoteknik för att tillverka ett 1D-gitter av kopplade icke-linjära resonatorer," förklarade Ravets och Bloch. "Varje resonator består av en optisk kavitet som innehåller ett aktivt medium (en halvledarkvantbrunn), som tillhandahåller icke-linjäriteten. Kopplingen mellan angränsande kaviteter är förskjuten för att implementera den enklaste topologiska modellen, känd som Su Schrieffer Heger-modellen."
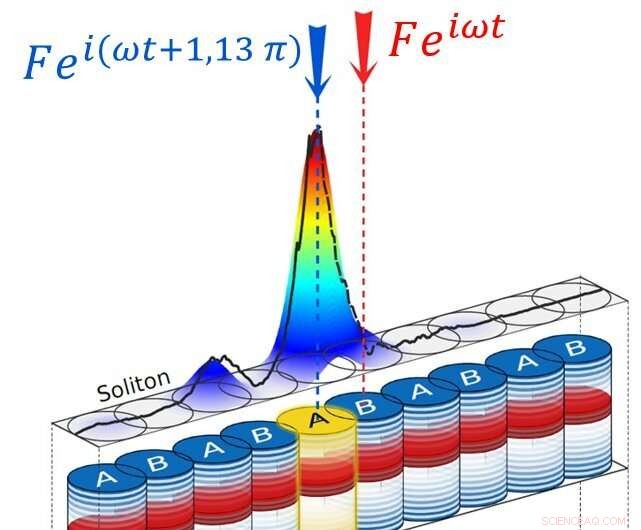
Illustration av den nya familjen av dissipativa gap-solitoner som upptäckts av forskarna för den uppmätta intensitetsprofilen för sådan soliton visas överst i figuren. Intensiteten är mycket stark på en enda plats, vilket leder till den spektrala avstämningen av denna plats i förhållande till resten av kedjan. Kedjan bryts alltså effektivt och ett kanttillstånd uppträder i excitationsspektrumet, som visas längst ner i figuren. Kredit:C2N/CNRS.
För att utlösa ett icke-linjärt svar i deras 1D-gitter, strålade Ravets, Bloch och deras kollegor en eller två laserstrålar på specifika delar av gittret. Därefter övervakade de den överförda intensiteten som en funktion av den ingående lasereffekten.
"En särskilt relevant ratt som vi använde i vårt experiment är den relativa fasen mellan excitationsstrålarna, vilket ger en ny nivå av kontroll som hittills inte har övervägts," sa Ravets och Bloch.
De experiment som forskarna utförde gav nya och intressanta resultat. Specifikt upptäckte teamet bildandet av nya gap soliton-familjer, som stabiliseras av resonansexitation. Dessa gapsolitoner existerar inte i konservativa system, såsom kopplade vågledare som arbetar i utbredningsgeometrier.
"Dessa solitoner har samma profil som ett topologiskt kanttillstånd och inducerar faktiskt uppkomsten av ett topologiskt kanttillstånd för excitationer ovanpå det olinjära stabila tillståndet. Vi vill kalla denna förmåga att styra systemet genom konstruktionen av laserexcitationen system "drivteknik", sa Ravets och Bloch.
Den nyligen genomförda studien av Ravets, Bloch och deras kollegor belyser möjligheten att utnyttja koherent drivning för att stabilisera olinjära faser i topologiska fotoniska system. I framtiden kan de experimentella metoderna som beskrivs i deras uppsats användas för att kontrollera topologin för 1D-fotoniska system och kan även utvidgas till 2D-system.
"I vår nästa studie planerar vi att utvidga dessa idéer till fotoniska topologiska isolatorer i 2D-gitter där vårt mål kommer att vara att demonstrera förmågan att optiskt styra topologin för ett icke-linjärt fotoniskt gitter genom konstruktionen av drivningen och spridningen." Ravets och Bloch tillade. + Utforska vidare
© 2022 Science X Network