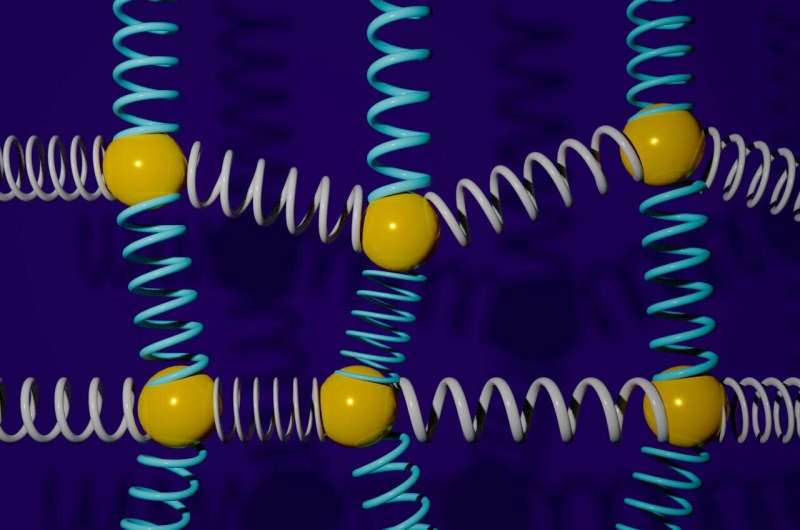
Även om "kopplade oscillationer" kanske inte låter bekant, finns de överallt i naturen. Termen "kopplade harmoniska oscillatorer" beskriver interagerande system av massor och fjädrar, men deras användbarhet inom vetenskap och teknik slutar inte där. De beskriver mekaniska system som broar, bindningarna mellan atomer och till och med gravitationella tidvatteneffekter mellan jorden och månen. Genom att förstå sådana problem kan vi undersöka ett motsvarande stort utbud av system från kemi till teknik till materialvetenskap och vidare.
Klassiskt representerade av en kul- och fjädermodell blir kopplade oscillatoriska system allt mer komplexa när fler oscillatorer läggs till. Med en ny kvantalgoritm som delvis skapats av Pacific Northwest National Laboratory (PNNL) och professor Nathan Wiebe vid University of Toronto, är simulering av sådana komplexa kopplade oscillatorsystem nu snabbare och effektivare. Dessa resultat publicerades i Physical Review X .
Tillsammans med forskare från Google Quantum AI och Macquarie University i Sydney, Australien, utvecklade Wiebe en algoritm för simulering av system med kopplade massor och fjädrar på kvantdatorer. Forskarna gav sedan bevis på den nya algoritmens exponentiella fördel jämfört med klassiska algoritmer.
Denna snabbhet möjliggjordes genom att kartlägga dynamiken hos de kopplade oscillatorerna till en Schrödinger-ekvation - kvantmotsvarigheten till en klassisk Newtonsk ekvation. Därifrån kunde systemet simuleras med Hamiltonska metoder.
I huvudsak tillåter detta tillvägagångssätt forskare att uttrycka dynamiken hos kopplade oscillatorer med mycket färre kvantbitar än traditionella metoder. Forskare kan sedan simulera systemet med exponentiellt färre operationer.
Den kanske mest spännande aspekten av deras arbete uppstår från frågan om denna algoritm verkligen erbjuder en exponentiell hastighetshöjning jämfört med alla möjliga vanliga algoritmer. Först visade författarna att denna algoritm fungerar åt båda hållen:att kopplade harmoniska oscillatorer kan användas för att simulera en godtycklig kvantdator.
Detta innebär att på en hög nivå kan mycket stora system av interagerande massor och fjädrar innehålla beräkningskraft som motsvarar en kvantdator.
För det andra övervägde författarna de teoretiska begränsningarna kring att beräkna denna dynamik. Om det fanns ett sätt att simulera denna dynamik i polynomtid på befintliga datorer, skulle forskare kunna konstruera en snabbare metod för att simulera kvantdatorer. Detta skulle dock bevisa att kvantdatorer i princip inte är mer kraftfulla än klassiska datorer.
Bevis som samlats under åren visar att det är exceptionellt osannolikt att klassiska datorer är kvalitativt lika kraftfulla som kvantdatorer. Således ger detta arbete ett övertygande argument för att denna algoritm ger en exponentiell hastighetsuppgång såväl som en tydlig demonstration av en ny och subtil koppling mellan kvantdynamik och den ödmjuka harmoniska oscillatorn.
"Väldigt få nya klasser av bevisbara exponentiella hastighetshöjningar av klassiska beräkningar har utvecklats," sa Wiebe. "Vårt arbete ger en betydande beräkningsmässig fördel för ett brett spektrum av problem inom teknik, neurovetenskap och kemi."
Mer information: Ryan Babbush et al, Exponential Quantum Speedup in Simulating Coupled Classical Oscillators, Physical Review X (2023). DOI:10.1103/PhysRevX.13.041041
Journalinformation: Fysisk granskning X
Tillhandahålls av Pacific Northwest National Laboratory