Att lägga till en enkel regel till ett idealiserat biljardspel leder till en mängd spännande matematiska frågor, såväl som tillämpningar i levande organismers fysik. Den här veckan har forskare från universitetet i Amsterdam, inklusive två masterstudenter som första författare – publicerat en artikel i Physical Review Letters om den fascinerande dynamiken i biljard med minne.
En idealiserad version av biljardspelet har fascinerat matematiker i decennier. Grundfrågan är enkel:När en biljardboll väl är spelad, var tar den vägen och var hamnar den? Anta att biljarden är perfekt:Väggarna är perfekt studsande, det finns inga andra föremål på bordet, bollens rörelse är friktionsfri och så vidare. Då kommer bollen inte riktigt att "sluta" någonstans; det kommer att fortsätta för alltid.
Men kommer den någonsin tillbaka där den började? Besöker den så småningom alla delar av bordet? När vi något ändrar bollens riktning, eller dess startplats, ser vägen den följer ut som den föregående?
Alla dessa frågor visar sig vara väldigt spännande ur en matematisk synvinkel. Deras svar är inte alltid kända - särskilt när formen på biljarden inte är enkel, som en kvadrat eller en rektangel. Till exempel, på triangulär biljard med hörn på mindre än 100 grader, är det känt att det alltid finns periodiska banor – banor som bollen kan följa och som återvänder till sig själva.
Detta kan bevisas matematiskt. Ändra nu ett av hörnen till en något större vinkel, och ingen matematiker vet svaret längre.
Idealiserade biljardspel är inte bara en favoritsysselsättning för matematiker. De har också en djupgående inverkan på fysik och andra vetenskaper. Många av frågorna om biljard kan formuleras som frågor om kaos:Gör liknande initiala förhållanden för ett dynamiskt system – oavsett om det är en boll på ett biljardbord, en molekyl i en gas eller en fågel i en flock – leder alltid till liknande slutgiltiga resultat?
I forskning utförd vid universitetet i Amsterdam har ett team av fysiker insett att genom att ändra reglerna för biljardspelet något ökar antalet ansökningar i den verkliga världen ytterligare.
Mazi Jalaal, medförfattare till publikationen och chef för gruppen där forskningen gjordes, förklarar:"I naturen har många levande organismer en extern form av minne. Till exempel lämnar de spår för att komma ihåg var de har varit. De kan sedan använda den informationen för att antingen följa samma rutt igen, eller – till exempel när de letar efter mat – för att inte utforska samma region igen."
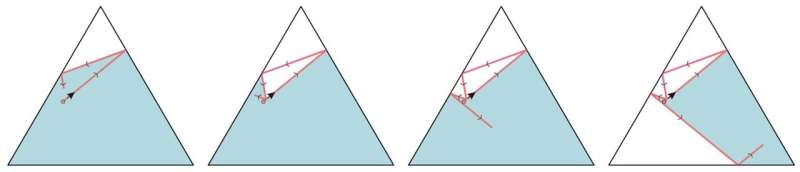
Det senare alternativet ledde forskarna till en intressant idé:Vad händer om vi lägger till en regel till biljardspelet, nämligen att bollen aldrig får korsa sin egen tidigare väg? Resultatet är att den effektiva storleken på biljardbordet blir mindre och mindre. Faktum är att bollen så småningom fångas av sin egen bana.
Spännande nya frågor
Fångningseffekten gör systemet ännu mer spännande. Även enkla frågor blir nu oerhört fascinerande. Hur långt färdas en boll innan den fastnar? Svaret varierar, både på bordets form och på bollens utgångspunkt och riktning.
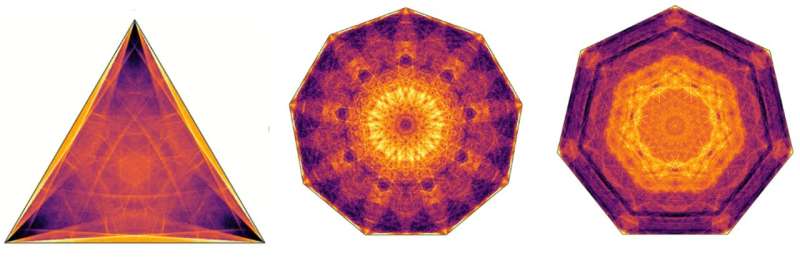
Ibland färdas bollen en längd som bara är några gånger så stor som bordet, ibland kan den gå 100 gånger så lång innan den fastnar. Var bollen så småningom hamnar i sitt fångade tillstånd är också en intrikat fråga; att upprepa experimentet på en dator miljontals gånger, varje gång med en något annorlunda startposition och hastighet, leder till vackra mönster av slutliga konfigurationer.
Bilden överst i denna text visar några av dessa vackra exempel. Intressant nog kan de resulterande dynamiska systemen vara kaotiska. Om du bara ändrar startpositionen eller hastigheten för den självundvikande bollen lite kan det leda till att den fastnar på en helt annan plats på biljarden.
Dessutom, i motsats till vad som händer på ett vanligt biljardbord, är det inte lika troligt att den självundvikande bollen hamnar var som helst. Vissa regioner är mer sannolika än andra. För att förklara och bevisa alla dessa särdrag, har matematikerna verkligen gjort sitt jobb.
En intressant egenhet med publikationen är att båda dess första författarna är masterstudenter. Jalaal tillägger, "Idén med en "biljard med minne" är enkel nog och ny nog att det inte kräver många års erfarenhet att studera den. Thijs och Stijn gjorde ett fantastiskt jobb med att göra materialet till sitt eget och hitta smarta sätt att studera alla dessa nya öppna problem. Jag är mycket glad att de redan kan vara huvudförfattare till en publikation."
Resultaten är bara de första stegen i vad som kan bli ett helt nytt forskningsområde. Det finns inte bara många intressanta matematiska frågor som nu väntar på att bli besvarade; tillämpningarna inom fysik, inklusive biofysik, är också oändliga.
Jalaal säger, "Konceptet med fångst är ett som ber att utforskas, även i verkliga system. Till exempel vet vi att encelliga slemformar använder självundvikande vägar. Blir de också instängda och vad händer när de gör eller har de smarta mekanismer för att undvika att detta händer överhuvudtaget. Använder de det för att förbättra sökstrategier för mat?
"Resultaten skulle hjälpa oss att bättre förstå dessa biologiska system, och kanske till och med införliva de lärdomar vi lär oss för att optimera denna form av biljard med minne för användning i robotar."
Mer information: Thijs Albers et al, Billiards with Spatial Memory, Physical Review Letters (2024). DOI:10.1103/PhysRevLett.132.157101. På arXiv :DOI:10.48550/arxiv.2307.01734
Journalinformation: Fysiska granskningsbrev , arXiv
Tillhandahålls av University of Amsterdam