
Hur mycket stress utsätts rören för när en vätska strömmar genom dem, och hur beror det på rörets krökningsgrad?
Böjningar i rör är särskilt avgörande, till exempel i aortabågen som ansluter till den vänstra ventrikeln i det mänskliga hjärtat. Rörsystem i industrianläggningar inkluderar ofta böjar på 90 grader eller mer, kan vara spiralformade och kan till och med ha 180-graders böjar. Vätskemekanister i Sverige har analyserat vätskeflödet i sådana rör med 180 graders böj. Deras forskning är publicerad i tidskriften Physical Review Fluids .
Böjningar i rör skiljer sig från deras raka sektioner eftersom det i de krökta sektionerna finns utåtriktade centrifugalkrafter på grund av trögheten hos vätskan inuti. Den kraften balanseras av en tryckgradient från rörets yttervägg till innerväggen. Eftersom vätskehastigheterna i en imaginär skiva genom röret inte kommer att vara lika i den krökta sektionen - till exempel kommer hastigheten nära rörets yttervägg att vara större än nära den inre väggen - ett sekundärt flödesmönster, förutom rörelsen genom röret, sätts upp vinkelrätt mot huvudflödesriktningen.
Denna rörelse är ett par motroterande, symmetriska virvlar, kallade Dean virvlar, efter den brittiska vetenskapsmannen William Reginald Dean, som dyker upp i den första kröken i röret och kan komplicera flödet efter, för både laminärt och turbulent flöde.
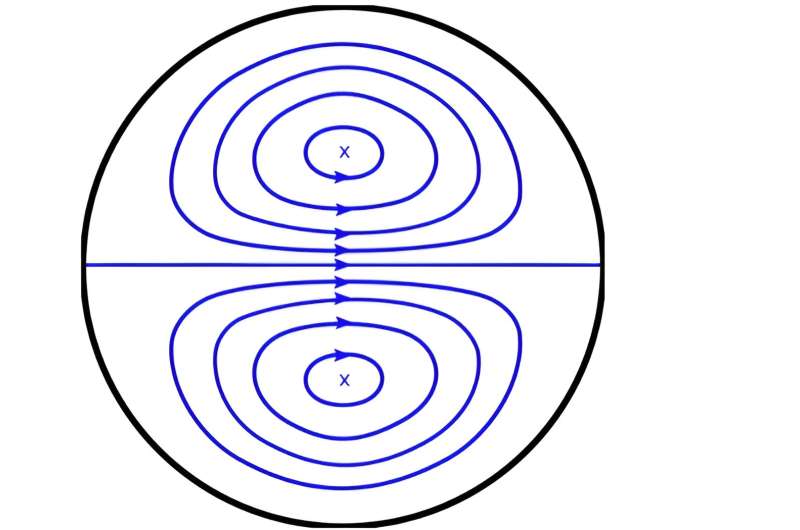
För en enskild böj kan flödets inre geometri beskrivas av Dean-talet, vilket beror på rörets radie i förhållande till krökningens storlek, och vätskans Reynolds-tal, som är förhållandet mellan tröghetskrafter till viskösa krafter i en vätska. Vätskor har ett kritiskt Reynolds-tal som kännetecknar deras övergång från jämnt, laminärt flöde till turbulent flöde, och detta kan vara dubbelt så stort som vid rakt flöde. (Faktum är att turbulent flöde från ett rakt rör kan återgå till laminärt när det kommer in i en spiralsektion av röret.)
Uppskattningsvis indikerar Reynolds siffror under 2 000 laminärt flöde, de över 3 500 turbulent flöde, med en övergång från laminärt till turbulent flöde någonstans däremellan. Dean-numret mäter intensiteten av det interna, sekundära flödet.

Daniele Massaro och kollegor vid Kungliga Tekniska Högskolan i Stockholm använde en förfinad metod för att numeriskt, beräkningsmässigt lösa de välkända komplicerade Navier-Stokes-vätskeekvationerna för att analysera övergången (från laminärt till turbulent flöde) i ett idealiserat rör med en böj på 180 grader, och jämför deras fynd med tidigare resultat för armbågsrör (90 graders böjning) och ringformade rör.
Om man antar en representativ rörkrökning på 1/3 - förhållandet mellan radien för ett tvärsnitt av röret och krökningsradien - delade gruppen den simulerade vätskan i cirka 30 miljoner galler, inte alla enhetliga. De löste sedan ekvationerna för rutnätspunkterna allteftersom de förändrades med tiden.
Genom att utföra en stabilitetsanalys – bestämma tillväxten av små, oändligt små defekter som uppträder i den initiala jämna vätskan – bestämmer beräkningen förändringarna i vätskan när den rundar kurvan. Förändringarna sker genom alla vertikala tvärsnitt av vätskan och längs rörets längd. På så sätt kan flödets övergång från laminärt till turbulent bestämmas.
Den intensiva beräkningen - för vilka superdatorer krävdes, sa Massaro, med körningar som kan ta månader - fann att det kritiska Reynolds-talet för övergången var 2 528. Detta är området för vätskans Reynolds-nummer, oavsett typ, där instabilitet uppstår och strukturens form leder till övergången till turbulens. Denna övergångspunkt är också känd som en "Hopf-bifurkation". Instabiliteten för 180-gradersböjen utvecklas ungefär som den för en 90-gradersböj. Det kritiska Reynolds-talet för en 90-graders böj är 2 531 och för en torus 3 290.
På grund av instabilitetens detaljerade karaktär förväntas rör med böjningar större än 180 grader vara lika, upp till en viss punkt. För rör med kortare krökar måste Hopf-bifurkationen försvinna när krökningsvinkeln närmar sig noll med flödet kvar laminärt. Gruppen uppskattar att bifurkationen försvinner vid en böj på cirka 20 grader.
Även om forskningen har uppenbara industriella tillämpningar, är förlängningen till hjärtat inte okomplicerad på grund av skillnaden mellan faktiskt blod och denna studies idealiserade flöde. "Vår studie hjälper till att förstå var en plötslig övergång i den, vanligtvis, laminära aortabågen kan inträffa", säger Massaro, medförfattare till studien och doktorand vid avdelningen för teknisk mekanik vid Kungliga Tekniska Högskolan i Stockholm . "Faktiskt kan den turbulenta regimen i aortan potentiellt relateras till olika hjärtsjukdomar."
Mer information: Daniele Massaro et al, Global stabilitet av 180∘ -böj rörflöde med mesh adaptivitet, Physical Review Fluids (2023). DOI:10.1103/PhysRevFluids.8.113903
Journalinformation: Fysiska granskningsvätskor
© 2023 Science X Network