Överskott av ytenergi från otillfredsställda bindningar är en betydande drivkraft för dimensionsförändringar i tunnfilmsmaterial, om bildandet av hål, sammandragande kanter, eller flyktiga hörn. I allmänhet, denna uppdelning av ett material kallas avvätning. Nyligen utexaminerad MIT Rachel V. Zucker, som disputerade den 5 juni, har utvecklat en rad matematiska lösningar för att förklara olika avvätningsfenomen i solida filmer.

Arbetar med medarbetare på MIT såväl som i Tyskland och Italien, Zucker, 28, utvecklat en modell för beräkning av helfacetterad kantindragning i två dimensioner, men hon säger att kronjuvelen i hennes arbete är en fasfältsmetod som ger en allmän metod för att simulera avvätning.

Tunnfilmsmaterial sträcker sig från cirka 1 mikrometer (mikron) ner till bara några nanometer i tjocklek. Filmer i nanometerskala är de grundläggande byggstenarna för kretskort i elektroniska och elektrokemiska enheter, och är mönstrade till trådar, transistorer, och andra komponenter. Zucker utvecklade modeller för vad som händer med tunna filmer över tid. "De har mycket yta jämfört med deras volym, bara för att de är så tunna, speciellt i en dimension, och så det kan faktiskt utgöra en enorm drivkraft för den tunna filmen att ändra sin form, " hon säger.

På MIT, Zucker fick råd av professorerna W. Craig Carter och Carl V. Thompson. Med avvätning, Zucker tacklade ett av de svåra problemen inom materialvetenskap, Carter förklarar, speciellt med tillägg av anistropisk ytspänning. "Ekvationer börjar se väldigt komplicerade ut och metoderna som du skulle använda för att lösa dessa ekvationer börjar bli mer och mer oklara. Och när du går den här vägen, du går in i terra incognita. Hur går du tillväga för att lösa dessa problem?"

Avvätning av fasta filmer ser ut som avvätning av en vätska - till exempel, vatten pärlar sig på en vindruta - men materialet förblir fast under denna process. Avvätning i fast tillstånd kan ske vid temperaturer långt under materialets smälttemperaturer när filmen är mycket tunn, och speciellt när den är mönstrad för att göra mycket små funktioner som ledningar i integrerade kretsar. "Avvätning i fast tillstånd börjar bli mer och mer av ett problem när vi gör saker med mindre och mindre funktioner, " säger Thompson.

Zucker studerade båda isotropa materialen, som uppvisar samma egenskaper i alla riktningar, och anisotropa material, som visar olika egenskaper i olika riktningar. Isotropa material, som vanligtvis är glasiga, är bra material för att utveckla modeller, men används sällan som ingenjörsmaterial, hon säger. Vanliga tekniska material som metall, keramisk, eller tunna enkristallfilmer är vanligtvis anisotropa material.

Zucker genomförde stabilitetsanalyser för att förstå början på de ibland vackra morfologierna som ses i experiment. "Den stora takeaway är:En, vi kan skriva ner formuleringen av detta problem; två, vi kan implementera en numerisk metod för att konstruera lösningarna; tre, vi kan göra en direkt jämförelse med experiment; och det slår mig som vad en avhandling borde vara – hela saken – formulering, lösning, jämförelse, slutsats, " säger Carter. Zucker försvarade sin avhandling, "Kapillärdriven formutveckling i solid-state mikro- och nanoskalasystem, "den 13 april.

Hon säger att hennes genombrott kom genom att skapa en geometrisk modell av kantindragning. "Jag visste att jag ville göra dessa stabilitetsanalyser; jag visste att jag ville förstå fingersättningsinstabiliteten och hörninstabiliteten, Rayleighs instabilitet, men jag visste inte var jag skulle börja, " säger Zucker. När hon insåg att hon kunde generalisera denna geometri och använda Wolfram Mathematica för att hantera algebra, hon kunde tillämpa det inte bara på kantindragning, men också för att utöka den till fingersättningsinstabiliteten och hörninstabiliteten. "Jag skulle säga att det var en användbar insikt, " tillägger hon, men noterar att det inte kom under arbetet, men när du springer under ett jullov. "Så plötsligt slog det mig, " förklarar hon.

Fasfältsmetod

För hennes doktorandforskning, Zucker undersökte filmuppbrytning under avvätning baserat på kapillärverkan för kantretraktion och nypning, fingersättningsinstabiliteten, Rayleighs instabilitet, och hörninstabiliteten. Denna kapillärverkan inträffar mest dramatiskt i en region som kallas trippellinjen, där tre faser möts, vanligtvis substratet, film som deponeras, och atmosfär. Undantaget, som inte kan förklaras med enbart kapillärverkan, är hålbildning, Zucker noterar. Med sin fasfältsmetod, Zucker säger, "Jag behöver inte göra förenklade antaganden. Jag behöver inte förenkla geometrin, till exempel. Det behandlar bara hela problemet. Det har varit två tidigare simuleringsförsök, skulle jag säga, men vår är den första koden som jag skulle säga är faktiskt användbar, eftersom det är tillräckligt snabbt för att det ska köras inom en rimlig tid på ett rimligt antal datorkärnor. Så vi kan faktiskt göra vetenskap med det." Simuleringar som brukade ta en månad på tidigare kod kan reduceras till ungefär tre dagar med hennes simulering, förklarar hon.

"Rachel gjorde mycket betydande framsteg i vår förståelse av fingersättningsinstabiliteten som utvecklas längs kanterna på filmer när de genomgår avvätning i fast tillstånd, " säger Thompson. "Medan folk hade spekulerat i att fälgarna som bildas på dessa kanter genomgår en Rayleigh-liknande instabilitet som leder till fingersättning, Rachel visade att en ny instabilitet hon upptäckte, på grund av "divergent indragning, ' spelar en dominerande roll. Detta möjliggör bättre förutsägelser av längdskalorna för strukturer som är resultatet av avvätningsprocessen, och för hur filmer kan modifieras för att erhålla strukturer med önskade egenskaper.

"Rachel gav också nya och bättre förklaringar av de mekanismer som gör att skarpa hörn i kanten av ett indragande hål rinner ut före andra delar av kanten. Spekulationer i litteraturen fokuserade på rollen av långdistansdiffusion av material bort från hörnet, men Rachel visade att all massa som omfördelas vid den indragande spetsen av ett hörn konsumeras lokalt för att förlänga längden på de intilliggande kanterna. Detta gav ett fundamentalt nytt sätt att tänka på utvecklingen av hålens former, och hur den utvecklingen kan kontrolleras, " förklarar Thompson.

Modellering av instabiliteter

Zucker tillbringade mycket tid med sin doktorsexamen i Tyskland, där hon var värd av professor Christina Scheu, vid Max Planck Institute for Iron Research i Düsseldorf och Ludwig-Maximilians University i München. Zucker tillbringade cirka nio månader i München följt av nio månader i Düsseldorf. Zucker tillskriver professor Axel Voigt vid Dresdens tekniska universitet i Tyskland mycket av kodutvecklingsarbetet för fasfältsimuleringar av avvätning, och postdoc Rainer Backofen. Hon krediterar också professor Francesco Montalenti vid universitetet i Milano-Bicocca i Italien, postdoc Roberto Bergamaschini, och doktoranden Marco Salvalaglio med att hjälpa henne lära sig hur man använder koden. I Tyskland, hon har också arbetat med mikrostrukturell optimering för energimaterial.

"Jag ville arbeta med dessa ytenergidrivna problem eftersom de är så grundläggande för materialvetenskap, " förklarar Zucker. Carter kopplade samman Zucker med Thompson, vars grupp hade gjort experiment inriktade på att utveckla en bättre förståelse för avvätning i fast tillstånd, både för att förhindra eller undertrycka det i vissa fall, och även att utveckla nya sätt att kontrollera det för att skapa specifika mönster i andra fall.

Zucker tacklade olika oegentligheter i tunnfilmsbildning, inklusive Rayleigh instabiliteter, kantindragning, fingersättning, och hörninstabilitet. I Rayleighs instabilitet, till exempel, en cylinder av material bryts upp till isolerade partiklar. Rayleighs instabilitet är ett klassiskt resultat som nu är 137 år gammalt. "Annars har de andra instabiliteterna som är involverade i avvätning av filmer inte riktigt studerats, Zucker säger om sitt arbete. "Jag har gjort många linjära instabilitetsanalyser för att förstå vilka våglängder som kommer att dyka upp i dessa instabiliteter, vilka längdskalor pratar vi om och hur det är kopplat till filmtjockleken."

Avvätning i fast tillstånd

Modellen Zucker utvecklat för tvådimensionell kantindragning för starkt anisotropa, tunna filmer med fulla sidor publicerades 2013 i tidskriften Comptes Rendus Physique ("Proceedings of Physics"). Zuckers modell överensstämde till stor del med experiment utförda av Alan Gye Hyun Kim i Thompsons grupp på kantretraktion av 130 nm tjock, enkristall nickelfilmer på magnesiumoxid (MgO). Zucker var också medförfattare till Kims experimentella uppsats 2013 i Journal of Applied Physics. Både experiment och modell visade att fälgar bildades när kanterna dras tillbaka.

I en heltäckande film, kristallmaterialet har facetter som liknar en juvelslipad diamant. Zucker, som studerade fyra olika orienteringar av kristallstrukturen, fann att diffusiviteten på facetten längst upp på kanten har störst inflytande på indragningen, följt av influenser från materialets andra aspekter. Både experiment och modellen visade indragningsavstånd som varierade med upp till två gånger, beroende på kantriktningen. Modellen överensstämde närmast med experimentella resultat för en (001) film med en kant som dras tillbaka i (100) riktningen – varierande med bara 10 procent. Dock, Zuckers papper noterade, modellens överskattade indragningsavstånd för (001) film indragning i (110) riktning och underskattat avstånd för en (011) film indragning i (110) riktning. Zucker föreslår att diskrepansen mellan modell och experiment kan förklaras av fel i rapporterade värden på diffusiviteter för nickelfacetter och osäkerhet om gränsytenergi mellan nickelfilmen och magnesiumoxidsubstrat. "De viktigaste faktorerna som bestämmer indragningshastigheten för en tunn film, enligt denna modell, är:filmtjockleken, den atomära diffusiviteten på den övre facetten och den vinklade facetten, filmens ekvivalenta kontaktvinkel på substratet, och ytenergins absoluta värde. Kantindragningsavståndet skalar med filmtjockleken h som h1/2, Zucker rapporterade i "En modell för avvätning i fast tillstånd av en heltäckande tunn film."

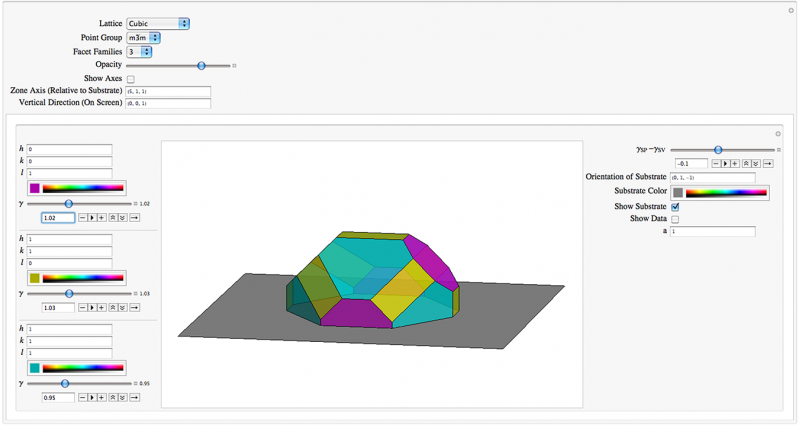
WulffMaker programvara

I en tidning från 2012, Zucker presenterade en ny metod för att hitta jämviktsformerna hos facetterade partiklar fästa på en deformerbar yta. Med Carter och tre andra, Zucker presented a suite of software tools to calculate these equilibrium shapes as well as for isolated particles and for particles attached to rigid interfaces. Their open-source code, WulffMaker, is available as a Wolfram computable document format file or a Mathematica notebook. It is useful for modeling Wulff shapes for engineering materials such as alumina, as well as more complicated Winterbottom and double Winterbottom shapes. While the Wulff method models the simplest case of a uniform shape attaching to a level surface, the software also incorporates a new algorithm for calculating interfaces with more complicated angles of attachment and attachment to rigid substrates. The tool could be useful for analyzing electronic and optical devices produced from materials deposited on a substrate. The software combines interface energy data with geometric shape data and so can be used in reverse to calculate interface energy for abutting materials from experimentally obtained geometric data.

"This tool introduces a new computational method for finding shapes of minimal interface energy. It also helps to build intuition about the macroscopic properties of interfaces and their interactions, and aids in the quantitative measurement of interface energy densities, given a geometry. Properties such as the equivalent wetting angle, particle contact area, total energies, and distortions to the interface surrounding the particle are displayed by the software to enable further insight and analysis, " Zucker wrote in her thesis.

Teaching modules

Besides her work in creating computerized models for thin film deformation, Zucker has been working with Carter on a new format to teach materials science that Carter calls proctored scaffolding. Unlike online instruction that allows students to passively consume information by watching videos or reading text, their approach is interactive and requires critical thinking. "The student can't just skate by without doing that critical thinking, " Zucker explains.

Zucker used the method, which integrates the Wolfram Language, to teach 3.016 (Mathematics for Materials Science and Engineers) two years ago while Carter was on sabbatical. She has traveled internationally with Carter to demonstrate these materials science master classes. They also made a user interface tool for content developers, to make it easier for other instructors to create Mathematica notebooks.

A native of North Carolina, Zucker completed her bachelor's at MIT in 2009, receiving an outstanding senior award from the Department of Materials Science and Engineering. Zucker starts a three-year postdoctoral fellowship in July at the Miller Institute at the University of California at Berkeley. She will be affiliated with both the mathematics and materials science departments. "I think ever since I was born I was going to be a professor, " Zucker says.

Den här historien återpubliceras med tillstånd av MIT News (web.mit.edu/newsoffice/), en populär webbplats som täcker nyheter om MIT-forskning, innovation och undervisning.