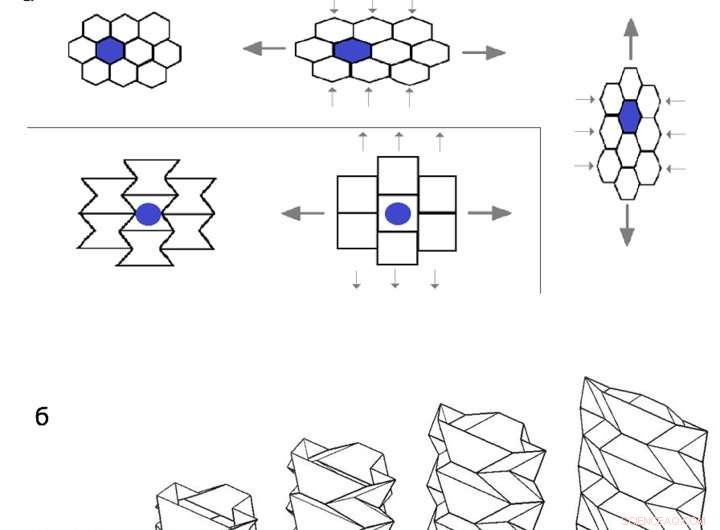
a) Vikta element av auxetiska material rätas ut, öka sin tvärgående dimension under sträckning. b) Produkter av material, vikt enligt reglerna för miura-ori:ett fällsystem, vilket gör det möjligt att räta upp konstruktionen i en rörelse, har också auxetiska egenskaper. c) Sneakersula som består av överlappande trianglar beter sig som ett auxetikum under tryck. Kredit:Artikelförfattare
En grupp forskare, inklusive specialister från Landau Institute for Theoretical Physics (ITF), har beskrivit en universell egenskap där många unika grafenegenskaper är "dolda". Onormalt grafenbeteende kan karakteriseras fullt ut av Poisson -förhållandet, som bestämmer ett materials förmåga att krympa eller sträcka sig i en tvärgående dimension. Dessutom, forskare hittade nyckelfaktorer som kan påverka denna egenskap. Resultaten publiceras i Fysisk granskning B .
Grafen är ett tvådimensionellt ark som består av ett lager kolatomer. En av de mest intressanta sakerna med grafen är förhållandet mellan dess unika elastiska och elektriska egenskaper. Till exempel, grafen visar extremt hög rörlighet för elektriska laddningar, som kan förändras drastiskt under elastisk stress. Fysiker försökte hitta en universell fysisk egenskap som helt återspeglar detta ovanliga beteende. Detta skulle göra det möjligt att använda grafen mer effektivt, samt skapa nya material med erforderliga exotiska egenskaper. Dock, tills nyligen kunde forskare inte hitta någon sådan parameter.
Nyckeln till att förstå denna fråga ljög i det ovanliga beteendet hos grafen under sträckning. De vanligaste materialen krymper i tvärriktning vid sträckning:ett gummiband är ett typiskt exempel. Dock, för ungefär hundra år sedan, den tyska fysikern Voldemar Voight upptäckte att pyritkristaller, tvärtom, sträcka sig under sträckning. Sådana material kallades auxetics, och i slutet av 1970 -talet fick forskare första konstgjorda auxetika. Hemligheten med sådana material kommer från deras ovanliga geometri. Även om i ett avslappnat tillstånd är auxetiska strukturelement vikta, när stretching appliceras utvecklas de och växer i storlek.
Auxetics har ett antal ovanliga funktioner som hjälper till att förbättra befintlig teknik och skapa ny. "Konventionella material expanderar vid uppvärmning och detta försämrar deras ursprungliga egenskaper genom olika mekaniska påfrestningar och störningar. Auxetik kan, tvärtom, krympa. Så det finns en idé att skapa kombinerade material med noll expansionskvot med hjälp av auxetics. När temperaturen stiger, den konventionella föreningen av sådana material tenderar att expandera, men auxetisk förening kommer att kompensera för detta, "kommenterar Valentin Kachorovskii, en ledande forskare vid The Ioffe Institute och ITF.
Den egenskap som bestämmer materialets förmåga att krympa eller sträcka sig i tvärgående dimension under spänning kallas Poisson -förhållandet. I auxetics är det negativt, i vanligt material - positivt. "Forskare var länge intresserade av grafen Poisson -förhållande, "säger Kachorovskii." Länge trodde vi att det var lika med det universella negativa värdet -?. Dock, ett antal senaste numeriska beräkningar visade att grafen Poisson -förhållandet kan vara både positivt och negativt. Vid första ögonkastet, resultat från olika beräkningar motsäger varandra fullständigt. "
Direkt experimentell verifiering av denna parameter är svårt. Grafen är svårt att få isolerat:den "odlas" vanligtvis på olika underlag, och deras egenskaper maskerar det verkliga värdet av grafen Poisson -förhållande. Vad är mer, prover av isolerad grafen är så små att det är praktiskt taget omöjligt att fästa fästen för kontrollerad sträckning. På samma gång, forskare och ingenjörer som utvecklar ny kolbaserad teknik behöver veta exakt om grafen är auxetiskt eller inte.
Författare till det nya verket lyckades "förena" motsägelsefulla resultat från tidigare beräkningar och hitta parametrar som exakt bestämmer Poisson -förhållandet mellan grafen. Fysiker fick reda på att det är ett variabelt värde beroende på dragkraft som appliceras. "Med en mycket stor kraft, grafen beter sig som ett normalt material, visar ett positivt Poisson -förhållande. Dock, när den applicerade kraften minskar, vi befinner oss i ett område där grafen uppvisar typiskt auxetiska egenskaper, "konstaterar Kachorovskii.
Forskare förklarade denna ovanliga koppling mellan Poisson -förhållande och stretching. På populära bilder visas grafen som ett tvådimensionellt ark med kolatomer, oftast platt. Dock, i verkligheten löper så kallade böjvågor längs detta "ark". De tenderar att förvandla grafen från ett plant tillstånd till ett skrynkligt tillstånd. "Detta kallas för en skrynklig övergång, "Kachorovskii förklarar." Under en lång tid förutspådde teorin om membran att på grund av detta fenomen tvådimensionella kristaller som grafen i princip inte kunde existera. De strävar alltid efter att krympa till en boll. Som vi ser, detta antagande var ett misstag eftersom vanliga komprimeringsförlängningsvågor längs grafens yta löper tillsammans med böjande. Olinjär interaktion mellan två vågtyper tillåter inte att membranet krymper till en boll. Även om, dimensionen av sådana kristaller är faktiskt inte lika med två. På grund av skrynklig övergång, det är i ett mellanläge mellan två och tre dimensioner. "
Membran som strävar efter att krulla på grund av vanliga kompressionsförlängningsvågor konkurrerar med effekten av utjämning av tvärgående vågor på grund av en extern applicerad kraft. Detta resulterar i ett förändrat tecken på Poisson -förhållandet. Med andra ord, om den yttre kraften är hög, de onormala auxetiska egenskaperna undertrycks och Poisson -förhållandet är positivt. Som forskarna visade, de ovanliga egenskaperna hos grafen baseras på det något skrynkliga viloläget. "I veck av tvärgående böjvågor lagras ytterligare energi, som står för grafen onormal elasticitet och andra ovanliga egenskaper. Till exempel, när upphettad grafen börjar krympa i längdriktningen, eftersom hela förlängningen går till tvärveck, "säger Kachorovskii." Och universell egenskap som bestämmer exakt grafenbeteende är Poisson -förhållandet. Med dess hjälp, du kan beskriva och förutsäga ett stort antal egenskaper hos grafen och andra material. "
Vad är mer, nuvarande arbete innehåller förklaring till varför tidigare studier av Poisson -förhållandet mellan grafen hade motsägelsefulla resultat. "Vi härledde ett analytiskt komplett ekvationssystem för den elastiska balansen i grafenark. Det visar sig att det finns två beteendemetoder för grafenmembran. I det vanliga, alla egenskaper hos grafen bestäms med standardformler och Poisson -förhållandet är positivt. På samma gång, för prover större än så kallad Ginzburg-längd, en onormal elasticitetsregim uppnås, vilket leder till ett negativt Poisson -förhållande, "tillägger Kachorovskii. För grafen, Ginzburgs längd varierar från 40 till 70 ångström. Storleken på prover som används i praktiken är säkert större, därför är det möjligt att se det mest ovanliga auxetiska beteendet.
Förklaringen av detta fenomen är också kopplad till vågor av olika typer, som interagerar med varandra på ett mycket komplicerat sätt. "Ginzburg -längden kännetecknar den skala i vilken dessa interaktioner inte längre kan försummas när de börjar flytta materialet onormalt. Till exempel, sådan storskalig interaktion tillåter inte att tvådimensionella kristaller krymper till en boll, "förklarar Kachorovskii. Olika ämnen har olika Ginzburglängder och att känna till dem är oerhört viktigt för utvecklingen av nya material." Ofta skapar människor nya material utan att beräkna Ginzburg -längden och sedan försöker de hitta något ovanligt i sina egenskaper. Men vårt arbete visar att om Ginzburg -längden är så stor som 1 kilometer, till exempel, vanliga storlekar visar inga speciella egenskaper, "Noterar Kachorovskii.
Det faktum att grafen kan töjas normalt eller onormalt beroende på den applicerade kraften i perspektiv hjälper till att skapa överkänsliga ljudsensorer, till exempel. "Ljudvågor sträcker grafenmembran, och beroende på sträckningsgraden ändrar grafen märkbart det elektriska motståndet. Beräkningar visar att känsligheten hos en sådan detektor kan vara gigantisk. Dessutom, i auxetik är ljudhastigheten märkbart högre än i "normala" material. Värdet av andra elastiska konstanter, till exempel, den unga modulen förblir densamma. Därför, när grafen sträcks till auxetiskt tillstånd, ljudet i det sprids mycket snabbt. Detta gör att vi kan skapa ultrasnabba sensorer som kan upptäcka en mycket snabb förändring av svängningar, säger Kachorovskii.