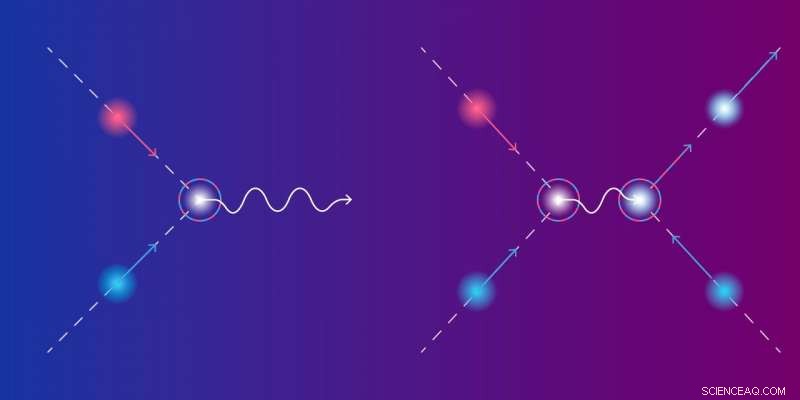
Två scenarier för elektron-hålsrekombination i grafen. Vid strålningsrekombination (vänster), ömsesidig förintelse av en elektron och ett hål, visas som blå respektive röda sfärer, frigör energi i form av en foton, en del ljus. I Auger-rekombination (höger), denna energi plockas upp av en elektron som passerar. Auger-processen är skadlig för halvledarlasrar, eftersom det förbrukar den energi som skulle kunna användas för att producera laserljus. Under en lång tid, Auger-processen ansågs vara omöjlig i grafen på grund av lagarna för bevarande av energi och momentum. Kredit:Elena Khavina/MIPT
Forskare från Moscow Institute of Physics and Technology och Tohoku University (Japan) har förklarat det förbryllande fenomenet med partikel-antipartikelförintelse i grafen, erkänd av specialister som Auger -rekombination. Även om det ihållande observerats i experiment, det ansågs under lång tid vara förbjudet av de grundläggande fysiska lagarna för energi och momentumbevarande. Den teoretiska förklaringen av denna process har tills nyligen förblivit ett av de största gåtorna inom fasta tillståndets fysik. Teorin som förklarar fenomenet publicerades i Fysisk granskning B .
1928, Paul Dirac förutspådde att en elektron har en tvillingpartikel, som är identisk i alla avseenden men för sin motsatta elektriska laddning. Denna partikel, kallas positron, upptäcktes snart experimentellt. Flera år senare, forskare insåg att laddningsbärarna i halvledare - kisel, germanium, galliumarsenid, etc. — beter sig som elektroner och positroner. Dessa två typer av laddningsbärare i halvledare kallades elektroner och hål. Deras respektive avgifter är negativa och positiva, och de kan kombineras igen, eller förinta varandra, släpper ut energi. Elektronhålsrekombination åtföljd av ljusutsläpp ger driftsprincipen för halvledarlasrar, som är viktiga enheter för optoelektronik.
Emissionen av ljus är inte det enda möjliga resultatet av att en elektron kommer i kontakt med ett hål i en halvledare. Den frigjorda energin går ofta förlorad till termiska vibrationer från närliggande atomer eller tas upp av andra elektroner (figur 1). Den senare processen kallas Auger-rekombination och är den huvudsakliga "dödaren" av aktiva elektron-hål-par i lasrar. Det bär namnet på den franske fysikern Pierre Auger, som studerade dessa processer. Laseringenjörer strävar efter att maximera sannolikheten för ljusemission vid elektron-hålsrekombination och att undertrycka alla andra processer.
Således, optoelektronikgemenskapen hälsade entusiastiskt förslaget om grafenbaserade halvledarlasrar som formulerats av MIPT-utexaminerade Victor Ryzhii. Det ursprungliga teoretiska konceptet sa att Auger-rekombination i grafen borde förbjudas av lagarna för bevarande av energi och momentum. Dessa lagar är matematiskt lika för elektron-hål-par i grafen och för elektron-positron-par i Diracs ursprungliga teori, och omöjligheten av elektronpositronrekombination med energiöverföring till en tredje partikel har varit känd länge.
Dock, experiment med heta laddningsbärare i grafen gav konsekvent det ogynnsamma resultatet:Elektroner och hål i grafen rekombinerar med en relativt hög hastighet, och fenomenet verkade hänföras till Auger-effekten. Dessutom, det tog ett elektron-hålpar mindre än en pikosekund, eller en biljondels sekund, att försvinna, vilket är hundratals gånger snabbare än i samtida optoelektroniska material. Experimenten antydde ett tufft hinder för implementeringen av en grafenbaserad laser.
Forskarna från MIPT och Tohoku University fann att rekombinationen av elektroner och hål i grafen, förbjudet enligt de klassiska bevarandelagarna, möjliggörs i kvantvärlden av principen om energitid-osäkerhet. Den anger att bevarandelagar kan överträdas i den utsträckning som är omvänt proportionell mot den genomsnittliga lediga tiden för partikeln. Den genomsnittliga lediga tiden för en elektron i grafen är ganska kort, eftersom de täta bärarna bildar ett starkt interagerande "mos". Att systematiskt redogöra för osäkerheten i partikelenergi, den så kallade nonequilibrium Green's functions-tekniken utvecklades inom modern kvantmekanik. Detta tillvägagångssätt användes av författarna till artikeln för att beräkna Auger-rekombinationssannolikhet i grafen. De erhållna förutsägelserna överensstämmer väl med experimentella data.
"I början, det såg ut som en matematisk hjärnpirring, snarare än ett vanligt fysiskt problem, säger Dmitrij Svintsov, chef för Laboratory of 2-D Materials for Optoelectronics vid MIPT. "De allmänt accepterade bevarandelagarna tillåter rekombination endast om alla tre inblandade partiklar rör sig exakt i samma riktning. Sannolikheten för denna händelse är som förhållandet mellan volymen av en punkt och volymen av en kub - den närmar sig noll. Som tur är, vi bestämde oss snart för att förkasta abstrakt matematik till förmån för kvantfysik, som säger att en partikel inte kan ha en väldefinierad energi. Detta innebär att sannolikheten i fråga är begränsad, och till och med tillräckligt hög för att kunna observeras experimentellt"
Studien ger inte bara en förklaring till varför den "förbjudna" Auger-processen faktiskt är möjlig. Viktigt, den specificerar villkoren när denna sannolikhet är tillräckligt låg för att göra grafenbaserade lasrar livskraftiga. När partiklar och antipartiklar snabbt försvinner i experiment med heta bärare i grafen, lasrarna kan utnyttja lågenergibärarna, som borde ha längre livslängder, enligt beräkningarna. Under tiden, det första experimentella beviset för lasergenerering i grafen har erhållits vid Tohoku University i Japan.
I synnerhet, metoden för beräkning av elektronhålslivslängderna som utvecklats i tidningen är inte begränsad till grafen. Det är tillämpligt på en stor klass av så kallade Dirac-material, där laddningsbärare beter sig på samma sätt som elektronerna och positronerna i Diracs ursprungliga teori. Enligt preliminära beräkningar, kvantbrunnarna för kvantsilverkadmiumtellurid skulle kunna möjliggöra mycket längre bärarlivslängder, och därför mer effektiv lasergenerering, eftersom bevarandelagarna för Auger-rekombinationer i detta fall är strängare.