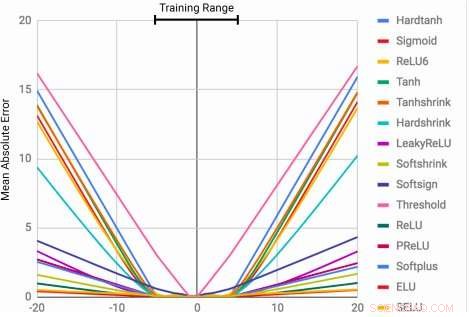
MLP:er lär sig identitetsfunktionen endast för de intervallvärden de är tränade på. Medelfelet ökar kraftigt både under och över intervallet för siffror som ses under träning. Kredit:Trask et al.
Förmågan att representera och manipulera numeriska storheter kan observeras hos många arter, inklusive insekter, däggdjur och människor. Detta tyder på att grundläggande kvantitativa resonemang är en viktig komponent i intelligens, som har flera evolutionära fördelar.
Denna förmåga kan vara ganska värdefull i maskiner, möjliggör snabbare och effektivare slutförande av uppgifter som involverar nummermanipulation. Än, än så länge, neurala nätverk som tränats för att representera och manipulera numerisk information har sällan kunnat generaliseras långt utanför intervallet av värden som möter under träningsprocessen.
Ett team av forskare på Google DeepMind har nyligen utvecklat en ny arkitektur som tar itu med denna begränsning, uppnå bättre generalisering både inom och utanför intervallet av numeriska värden som det neurala nätverket tränades på. Deras studie, som förpublicerades på arXiv, skulle kunna informera utvecklingen av mer avancerade verktyg för maskininlärning för att slutföra kvantitativa resonemangsuppgifter.
"När vanliga neurala arkitekturer tränas att räkna till ett tal, de kämpar ofta för att räkna till en högre, "Andrew Trask, ledande forskare i projektet, berättade för Tech Xplore. "Vi utforskade denna begränsning och fann att den sträcker sig till andra aritmetiska funktioner också, vilket leder till vår hypotes att neurala nätverk lär sig siffror som liknar hur de lär sig ord, som ett ändligt ordförråd. Detta förhindrar dem från att korrekt extrapolera funktioner som kräver tidigare osynliga (högre) siffror. Vårt mål var att föreslå en ny arkitektur som skulle kunna utföra bättre extrapolering."

Neural Accumulator (NAC) är en linjär transformation av dess ingångar. Transformationsmatrisen är den elementära produkten av tanh (Wˆ ) och σ(Mˆ ). Neural Arithmetic Logic Unit (NALU) använder två NAC:er med bundna vikter för att möjliggöra addition/subtraktion (mindre lila cell) och multiplikation/division (större lila cell), styrs av en grind (orange cell). Kredit:Trask et al.
Forskarna tog fram en arkitektur som uppmuntrar en mer systematisk sifferextrapolering genom att representera numeriska storheter som linjära aktiveringar som manipuleras med primitiva aritmetiska operatorer, som styrs av inlärda grindar. De kallade denna nya modul för den neurala aritmetiska logiska enheten (NALU), inspirerad av den aritmetiska logiska enheten i traditionella processorer.
"Siffror är vanligtvis kodade i neurala nätverk med antingen en-het eller distribuerade representationer, och funktioner över siffror lärs in inom en serie lager med icke-linjära aktiveringar, " Trask förklarade. "Vi föreslår att siffror istället ska lagras som skalärer, lagra ett enda nummer i varje neuron. Till exempel, om du vill lagra numret 42, du borde bara ha en neuron som innehåller en aktivering av exakt '42, ' istället för en serie med 0-1 neuroner som kodar för det."
Forskarna har också ändrat sättet på vilket det neurala nätverket lär sig funktioner över dessa siffror. Istället för att använda standardarkitekturer, som kan lära sig vilken funktion som helst, de utarbetade en arkitektur som framåt sprider en fördefinierad uppsättning funktioner som ses som potentiellt användbara (t.ex. tillägg, multiplikation eller division), använder neurala arkitekturer som lär sig uppmärksamhetsmekanismer över dessa funktioner.
"Dessa uppmärksamhetsmekanismer bestämmer sedan när och var varje potentiellt användbar funktion kan tillämpas istället för att lära sig den funktionen själv, " sade Trask. "Detta är en allmän princip för att skapa djupa neurala nätverk med en önskvärd inlärningsbias över numeriska funktioner."

(ovan) Ramar från tidsspårningsuppgiften gridworld. Agenten (grå) måste flytta till destinationen (röd) vid en angiven tidpunkt. (nedan) NAC förbättrar extrapoleringsförmågan som lärts av A3C-agenter för dateringsuppgiften. Kredit:Trask et al.
Deras test visade att NALU-förbättrade neurala nätverk kunde lära sig att utföra en mängd olika uppgifter, som tidsspårning, utföra aritmetiska funktioner över bilder av tal, översätta numeriskt språk till verkligt värderade skalärer, exekvera datorkod och räkna objekt i bilder.
Jämfört med konventionella arkitekturer, deras modul uppnådde betydligt bättre generalisering både inom och utanför intervallet av numeriska värden som den presenterades med under utbildningen. Även om NALU kanske inte är den perfekta lösningen för varje uppgift, deras studie ger en generell designstrategi för att skapa modeller som fungerar bra på en viss klass av funktioner.
"Föreställningen att ett djupt neuralt nätverk bör välja från en fördefinierad uppsättning funktioner och lära sig uppmärksamhetsmekanismer som styr var de används är en mycket utbyggbar idé, " Trask förklarade. "I detta arbete, vi utforskade enkla aritmetiska funktioner (tillägg, subtraktion, multiplikation och division), men vi är glada över potentialen att lära oss uppmärksamhetsmekanismer över mycket kraftfullare funktioner i framtiden, kanske ger samma extrapoleringsresultat som vi har observerat till en mängd olika områden."
© 2018 Tech Xplore