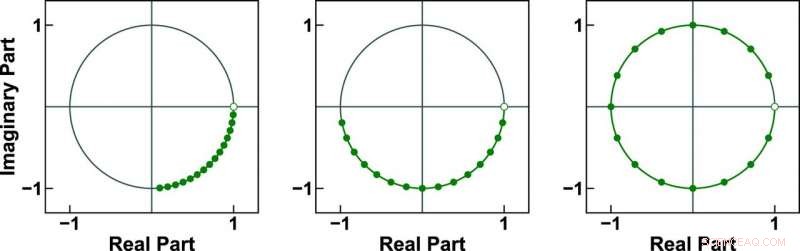
Här är tre exempel på 16-punkts chirp-konturer på enhetscirkeln. ICZT-algoritmen som utvecklats av Iowa State-ingenjörer kan fungera med alla tre medan den som tidigare användes endast kan fungera med den sista konturen. Kredit:Alexander Stoytchev.
Iowa State Universitys Alexander Stoytchev säger att det är en av de "mest populära och användbara" algoritmerna som finns – även om de flesta av oss aldrig har hört talas om det.
Men, om du har använt en mobiltelefon, surfade på internet eller behövde en medicinsk bild, du har dragit nytta av den snabba Fourier-transformen (FFT).
Transformen och dess invers (känd som IFFT) har använts sedan 1965. Till exempel, i din mobiltelefon används FFT för att analysera signalen som tas emot från basstationen (eller mobiltornet). IFFT löser det omvända problemet:den syntetiserar signalen som din telefon skickar till basstationen.
1969, forskare utvecklade en mer användbar, generaliserad version av FFT känd som chirp z-transform (CZT). Men ingen hade kommit med en generaliserad version av IFFT. Det var ett 50-årigt pussel i signalbehandling.
Det är, tills i höstas när två Iowa State-ingenjörer – Stoytchev och Vladimir Sukhoy – tillkännagav i en forskningsartikel att de hade kommit fram till en lösning i sluten form för den omvända chirp z-transformen (ICZT) och en snabb algoritm för att beräkna den. (Tidningen väckte ett stort intresse i signalbehandlingssamhället, uppgår till mer än 26, 000 åtkomster sedan oktober.)
Nu rapporterar Stoytchev – en docent i el- och datorteknik som också är knuten till universitetets Virtual Reality Applications Center – och Sukhoy – en lektor i elektro- och datorteknik – nya forskningsresultat om deras algoritm.
I en tidning som just publicerats online av Vetenskapliga rapporter , en Nature Research-tidskrift, de två visar hur deras algoritm fungerar "på enhetscirkeln, " som hänvisar till ett specialfall av dess parametrar. (Deras tidigare papper lyfte bara fram operationer "utanför enhetscirkeln.")
Papperet beskriver hur algoritmen kan arbeta med frekvenskomponenter som genereras av sampelpunkter från enhetscirkeln i det komplexa planet. Dessa punkter bildar en kontur som är känd som chirp-konturen. Till skillnad från IFFT, som endast kan fungera med provtagningspunkter med lika avstånd som helt täcker enhetscirkeln, ICZT-algoritmen kan arbeta med konturer som bara täcker en bråkdel av enhetscirkeln. Den kan också arbeta med konturer som sveper runt och utför flera varv över cirkeln. Detta möjliggör användning av vissa (icke ortogonala) frekvenskomponenter, vilket upphäver en av IFFT:s huvudrestriktioner och kan leda till bättre spektrumanvändning.
Uppsatsen identifierar de parametervärden för vilka algoritmen är numeriskt korrekt och för vilka den inte är det, och beskriver hur man uppskattar dess noggrannhet som en funktion av parametrarna. (Teknisk anmärkning:Den visar att singulariteterna för ICZT av storlek n är relaterade till elementen i Farey-sekvensen av ordning n-1. Detta är ett intressant samband eftersom Farey-sekvenser ofta förekommer i talteorin.)
Tidningen visar att på enhetscirkeln, ICZT-algoritmen uppnår hög noggrannhet med endast 64-bitars flyttal och kräver ingen ytterligare numerisk precision, gör det lättare att genomföra. Den rapporterar att algoritmen kan paras väl med den befintliga CZT-algoritmen för att göra back-to-back signalanalys och signalsyntes. Och det visar att algoritmen är snabb (den fungerar på vad som kallas O(n log n)-tid).
"Denna algoritm är mer generell än IFFT, men håller samma hastighet, sa Stoytchev.
Det är goda nyheter för ingenjörerna som arbetar med att lösa alla typer av signalbehandlingsutmaningar:
"Applikationsdomäner som kan dra nytta av detta, "skrev Iowa State ingenjörer i tidningen, "inkludera signalbehandling, elektronik, medicinsk bildbehandling, radar, ekolod, trådlös kommunikation, och andra."