
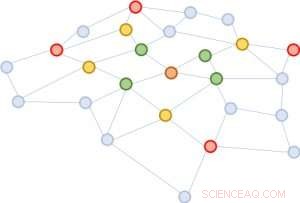
Figur 1:Utöka kvarteren med början från den bruna noden i mitten. Första expansionen:grön; andra:gul; tredje:röd.
En grafstruktur är extremt användbar för att förutsäga egenskaper hos dess beståndsdelar. Det mest framgångsrika sättet att utföra denna förutsägelse är att kartlägga varje entitet till en vektor genom att använda djupa neurala nätverk. Man kan sluta sig till likheten mellan två entiteter baserat på vektornärheten. En utmaning för djupinlärning, dock, är att man behöver samla information mellan en entitet och dess utökade grannskap över skikten av det neurala nätverket. Området växer snabbt, gör beräkningen mycket kostsam. För att lösa denna utmaning, vi föreslår ett nytt tillvägagångssätt, valideras genom matematiska bevis och experimentella resultat, som tyder på att det räcker att samla in informationen från endast en handfull slumpmässiga enheter i varje grannskapsexpansion. Denna avsevärda minskning av grannskapsstorleken ger samma kvalitet på förutsägelsen som toppmoderna djupa neurala nätverk men minskar utbildningskostnaderna i storleksordningar (t.ex. 10x till 100x mindre beräknings- och resurstid), leder till tilltalande skalbarhet. Vårt papper som beskriver detta arbete, "FastGCN:Snabbt lärande med Graph Convolutional Networks via Importance Sampling, " kommer att presenteras på ICLR 2018. Mina medförfattare är Tengfei Ma och Cao Xiao.
Komplexitet av grafanalys
Grafer är universella representationer av parvisa relationer. I verkliga applikationer, de finns i en mängd olika former, inklusive till exempel sociala nätverk, genuttrycksnätverk, och kunskapsgrafer. Ett trendämne inom djupinlärning är att utvidga den anmärkningsvärda framgången för väletablerade neurala nätverksarkitekturer för euklidisk strukturerad data (som bilder och texter) till oregelbundet strukturerad data, inklusive grafer. Graffalsningsnätverket, GCN, är ett sådant utmärkt exempel. Det generaliserar begreppet faltning för bilder, som kan betraktas som ett rutnät av pixlar, till grafer som inte längre ser ut som ett vanligt rutnät.
Tanken bakom GCN är väldigt enkel. De av oss som tog Signal Processing 101 eller en grundläggande datorseendekurs är redan bekanta med konceptet med ett faltningsfilter. För bilder, det är en liten matris av tal, multipliceras elementvis med ett rörligt fönster i bilden, med den resulterande produktsumman som ersätter fönstrets mittnummer. För grafer, detta är liknande. En bra kombination av filtren kan upptäcka primitiva lokala strukturer, såsom linjer i olika vinklar, kanter, hörn, och fläckar av en viss färg. För grafer, varvningar är likartade. Föreställ dig att varje grafnod initialt är fäst med en vektor. För varje nod, grannarnas vektorer summeras (med vissa vikter och transformationer) till den. Därav, alla noder uppdateras samtidigt, utför ett lager av framåtriktad fortplantning. Graffalsningar kan användas för att sprida information genom grannskap så att global information sprids till varje grafnod.
Problemet med GCN är att för ett nätverk med flera lager, kvarteret utökas snabbt, involverar många vektorer som ska summeras, för bara en enda nod. En sådan beräkning är oöverkomligt kostsam för grafer med ett stort antal noder. Hur stort kommer ett utökat kvarter att se ut? I sociala nätverksanalyser, det finns ett känt koncept myntat "sex grader av separation, " som säger att man kan nå vilken annan person som helst på jorden genom sex mellanliggande förbindelser! Figur 1 visar att från den bruna noden i mitten, utöka kvarteret tre gånger (i storleksordningen grönt, gul, och röd) kommer att röra nästan hela grafen. Med andra ord, Enbart uppdatering av vektorn för den bruna noden är besvärligt för en GCN med så få som tre lager.
Figur 2:Med utgångspunkt från samma bruna nod, i varje grannskapsexpansion, vi samplar endast fyra noder.
Förenkla för skalbarhet
Vi föreslår en enkel men kraftfull lösning, kallas FastGCN. Om det är kostsamt att bygga ut området fullt ut, varför inte utöka med bara ett fåtal grannar varje gång? Figur 2 illustrerar konceptet. Med utgångspunkt från den bruna noden, i varje expansion väljer vi ett konstant antal (fyra) noder och summerar endast vektorerna från dem. Provtagningen minskar avsevärt kostnaden för att träna det neurala nätverket, genom att minska utbildningstiden i storleksordningar på benchmarkdatauppsättningar som vanligtvis används av forskare. Än, förutsägelser förblir jämförelsevis korrekta. Storleken på dessa benchmark-diagram sträcker sig från några tusen noder till några hundra tusen noder, bekräftar skalbarheten av vår metod.
Bakom detta intuitiva tillvägagångssätt finns en matematisk teori för approximation av förlustfunktionen. Ett lager av nätverket kan sammanfattas som en matrismultiplikation:H'=s(AHW), där A är närliggande matris för grafen, varje rad av H är vektorn fäst vid noderna, W är en linjär transformation av vektorerna (även tolkad som modellparametern som ska läras in), och raderna av H' innehåller de uppdaterade vektorerna. Vi generaliserar denna matrismultiplikation till en integraltransform h'(v)=s(òA(v, u)h(u)W dP(u)) under ett sannolikhetsmått P. Sedan, provtagningen av ett fast antal grannar i varje expansion är inget annat än en Monte Carlo-approximation av integralen under måttet P. Monte Carlo-approximationen ger en konsekvent estimator av förlustfunktionen; därav, genom att ta gradienten, vi kan använda en standard optimeringsmetod (som stokastisk gradientnedstigning) för att träna det neurala nätverket.
En rad applikationer för djupinlärning
Vårt tillvägagångssätt tar itu med en viktig utmaning inom djupinlärning för storskaliga grafer. Det gäller inte bara GCN utan också många andra grafiska neurala nätverk byggda på konceptet med grannskapsexpansion, en viktig komponent i inlärning av grafrepresentationer. Vi förutser att lösningen av utmaningen i denna grundläggande datastruktur – grafer – kommer att användas i ett brett spektrum av tillämpningar, inklusive analys av sociala nätverk, den djupa insikten i protein-proteininteraktioner för läkemedelsupptäckt, och kuration och upptäckt av information i kunskapsbaser.