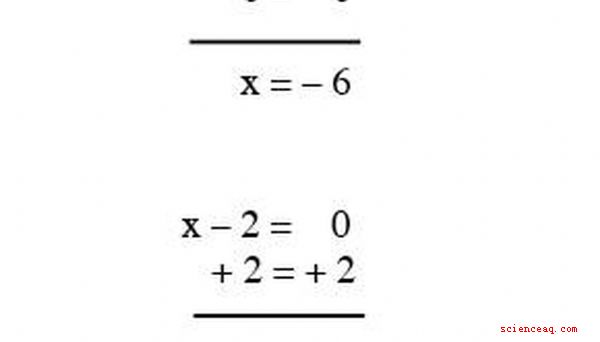
Faktoriserande ekvationer är en av grunden för algebra. Du kan hitta svaret på en komplex ekvation mycket lättare genom att bryta ekvationen ner i två enkla ekvationer. Även om processen kan verka utmanande först, är det faktiskt ganska enkelt. Du kommer i princip att bryta ekvationen ner till två enheter, som, när de multipliceras tillsammans, skapar ditt ursprungliga objekt. Du kan faktorera och lösa ekvationer helt enkelt i några få steg.

Ställ in din ekvation till 0. Säg att du presenteras med en ekvation som x ^ 2 + 7x = --12, du lägger till 12 för båda sidor av ekvationen att ställa in den till 0. När du har gjort det så ser din ekvation ut så här: x ^ 2 + 7x + 12 = 0.

Hitta faktorerna. I det här fallet handlar du nu om x ^ 2 + 7x + 12 = 0. Du skulle hitta faktorerna för 12. Faktorer av 12 inkluderar 1, 2, 3, 4, 6 och 12.

Gör säkerställ att dina faktorer lägger till den mellersta variabeln. Av alla faktorer som finns i steg 2, lägger bara 3 och 4 till 7, den mellersta variabeln. Se till att dina faktorer lägger till din centervariabel är viktig i factoring.

Faktorera dina okända variabler. Eftersom x är kvadrat, när du fakturerar det, kommer du att ha en x. Se nästa avsnitt för mer om hantering av okända variabler.

Skriv ut din nya ekvation. Eftersom 3 och 4 verkar vara rätt, skriver du ut din ekvation som (x + 3) (x + 4) = 0.

Lös. Nu kan du ställa in din ekvation för att lösa för x. I den här situationen skulle du ha x + 3 = 0 och x + 4 = 0. Båda dessa skulle visa att x = --3 och x = --4.

Kontrollera din ekvation genom att ersätta din x med dina lösningar: - 3 ^ 2 + 7 (- 3) + 12 = 0 9 + (--21) + 12 = 0 21 + (--21) = 0

- 4 ^ 2 + 7 (- 4) + 12 = 0 16 + (--28) + 12 = 0 28 + (--28) = 0

Ställ ekvationen på 0 och faktor ekvationen som du gjorde i steg 1 och 2 i det sista avsnittet om din ekvation har ett negativt numeriskt värde. Exempelvis kan du presenteras med en ekvation som x ^ 2 + 4x - 12 = 0.

Hitta faktorerna i x ^ 2 + 4x - 12 = 0. För denna ekvation är faktorerna 1, -1, 2, -2, 3, -3, 4, -4,6, -6, -12 och 12 för antalet 12. Eftersom din senaste variabel är negativ kommer dess faktorer att vara positiv och negativ. I den här situationen skulle 6 och -2 vara dina faktorer, som när de multipliceras tillsammans, har de en produkt av -12, och när de läggs ihop är deras produkt 4. Ditt svar kommer nu att se ut (x + 6) ( x - 2) = 0.

Lös för x som du gjorde i det sista avsnittet; x kommer att vara lika med -6 och 2. Se Figur 1.

Kontrollera din ekvation genom att placera dina lösningar i stället för x. (-6) ^ 2 + 4 (-6) - 12 = 0 36 + (-24) - 12 = 0 36 + (-36) = 0

2 ^ 2 + 4 (2) - 12 = 0 4 + 8 - 12 = 0 12 - 12 = 0

Tips

Du kan också följa dessa steg om du arbetar med en mindre ekvation, t.ex. som x ^ 2 + 5x = 0. Faktor ut x, som är gemensamt för båda variablerna, och löser x. x (x + 5) = 0. x kommer att vara 0 och -5.