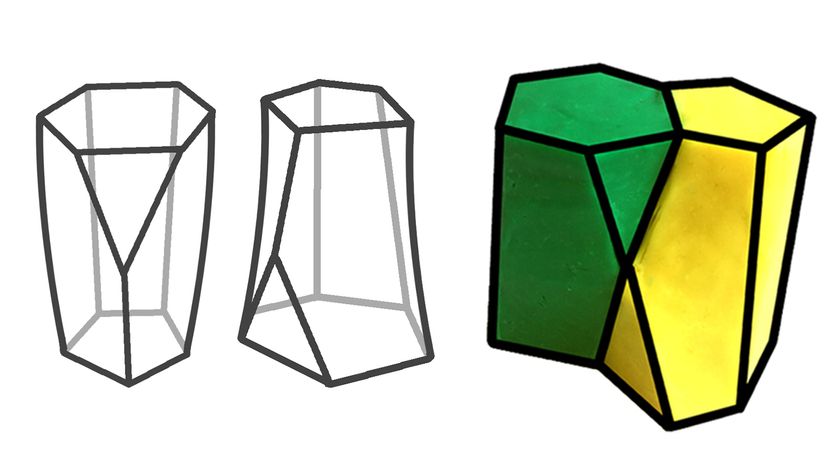
 Forskare upptäckte att epitelceller - de som täcker ytan på många mänskliga organ - använder en ny geometrisk form, scutoid, så vävnaderna kan kurva. University of Sevilla
Forskare upptäckte att epitelceller - de som täcker ytan på många mänskliga organ - använder en ny geometrisk form, scutoid, så vävnaderna kan kurva. University of Sevilla Om du inte har levt under en avlång sfäroid, du har säkert hört talas om den senaste upptäckten i former:scutoid. Ett team av spanska biologer från universitetet i Sevilla modellerade scutoid för att avgöra hur epitelceller packas ihop för att bilda hudens barriärer, organ och blodkärl.
Forskarna använde helt enkelt matematik för att hypotesera en form i naturen - en form som är nödvändig för konstruktion av flercelliga organismer. När det blev klart att formen var ny för geometri, de namngav det efter scutellum, den del av en skalbaggs bröstkorg som vagt liknar den nydöpta scutoiden.
I exemplet med scutoid, vi kan mycket intuitivt upptäcka nya former:varifrån de kommer och varför vi söker dem till att börja med.
Den mest grundläggande formen för formupptäckt är helt enkelt att se dem i den naturliga världen. Sexkanten (en sexsidig polygon), till exempel, förekommer i allt från såpbubblor och bikakor till Saturnus moln. Som författaren Phillip Ball utforskade i Nautilus -artikeln "Varför naturen föredrar hexagoner, "förklarar han hur det är en geometriskt idealisk form för ett antal funktioner. Som sådan, sexkanten kom från fysiska interaktioner och biologisk utveckling. Människor kom bara och gav den namnet.
Andra former är mindre vanliga i naturen men kommer lätt fram ur geometri - eller till och med oinformerad fantasi. Rätvinkliga, till exempel, är sällsynta i den naturliga världen. En promenad genom vildmarken kommer inte att ge dig torg och rektanglar. Verkligen, forskning tyder på att vi istället kan vara fastkopplade för att föredra naturliga kurvor framför raka linjer. Ändå konstruerar vi fortfarande kuber och använder dem för att göra om världen.
Det finns en koppling, dock, mellan de typer av former som kan konceptualiseras och de som kan hittas eller reproduceras i naturen. Perfekta cirklar, till exempel, existerar inte i vårt materiella område. Rent matematiskt sett, vi kan enkelt konstruera en uppsättning punkter i ett plan som är lika långt från en given punkt. Men, i verkligheten, även de mest fint utformade cirklarna och sfärerna saknar matematisk perfektion. Till och med de gyroskopiska kvartsrotorerna som byggts för NASA:s Gravity Probe B är fortfarande mindre än tre tio-milondels tum från perfektion.
Scutoid, dock, verkar faktiskt existera. Vi kanske inte kan ser den, men forskare har matematiskt modellerat det som en lösning för ett biologiskt problem. Som sådan, om vetenskapen en dag skulle överge scutoid till förmån för en annan lösning, själva formen fortsätter att existera geometriskt.
Så, att uppdatera, man kan upptäcka former genom att se dem i naturen, härleda sin existens i naturen eller genom en övning i ren matematik. Det är sällsynt idag, men formjägare hittar ibland en ny typ av femkant eller till och med en ny klass av fasta former.
Så för all del, gå ut och se vad du kan hitta - men tänk på att vi redan har en hel del matematiska former på filen. Den trapezo-rombiska dodekaedern är redan tagen-och Clickhole har dibs på Triquandle.
Nu är det omöjligtOptiska illusioner som Penrose -triangeln utnyttjar samma visuella tendenser som gör bakåtstående bokstäver till ett så enkelt misstag i grundskolan. A sid och a q är tydligt olika på papper, men om vi tolkar dem som 3D -bilder, då är de helt enkelt två vyer av samma objekt. Penrose -triangeln kan inte verkligt finns i 3D -rymden, men vi uppfattar det som ett 3D -objekt och denna förvirrande figur är fortfarande sammansatt i form av en triangel. Fortfarande, som Lionel och Roger Penrose bevisade, du burk upptäcka och namnge sådana föremål - även om Oscar Reutersvärd skapade det år tidigare.