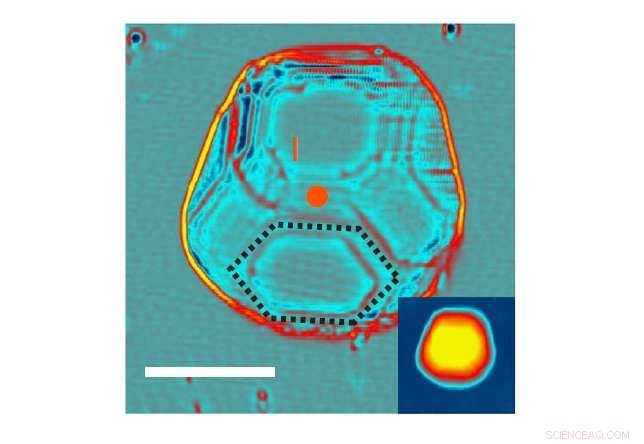
Topografisk bild av en bly -nanokristall som används i studien. Skalstapel:10 nm. Upphovsman:Vlaic et al. Naturkommunikation
För första gången, fysiker har experimentellt validerat en gissning från 1959 som sätter gränser för hur små superledare kan vara. Att förstå supraledning (eller avsaknaden därav) på nanoskala förväntas vara viktigt för att utforma framtida kvantdatorer, bland andra applikationer.
1959, fysikern P.W. Anderson gissade att supraledning endast kan existera i objekt som är tillräckligt stora för att uppfylla vissa kriterier. Nämligen, objektets supraledande gapenergi måste vara större än dess elektroniska energinivåavstånd - och detta avstånd ökar när storleken minskar. Avstängningspunkten (där de två värdena är lika) motsvarar en volym på cirka 100 nm 3 . Hittills har det inte varit möjligt att experimentellt testa Anderson -gränsen på grund av utmaningarna att observera supraledande effekter i denna skala.
I den nya studien publicerad i Naturkommunikation , Sergio Vlaic och medförfattare vid University Paris Sciences et Lettres och French National Center for Scientific Research (CNRS) designade ett nanosystem som gjorde att de experimentellt kunde undersöka Andersons gräns för första gången.
Anderson -gränsen uppstår eftersom, i mycket små skalor, de mekanismer som ligger till grund för supraledning slutar i huvudsak fungera. I allmänhet, supraledning uppstår när elektroner binder samman för att bilda Cooper -par. Cooper -par har en något lägre energi än enskilda elektroner, och denna skillnad i energi är den supraledande gapenergin. Cooper -parens lägre energi hämmar elektronkollisioner som normalt skapar motstånd. Om energin i den superledande luckan blir för liten och försvinner - vilket kan inträffa, till exempel, när temperaturen ökar - då fortsätter elektronkollisionerna och objektet slutar vara en superledare.
Anderson -gränsen visar att liten storlek är ett annat sätt att ett objekt kan sluta vara en superledare. Dock, till skillnad från effekterna av att höja temperaturen, detta beror inte på att mindre objekt har en mindre supraledande gapenergi. Istället, det uppstår för att mindre kristaller har färre elektroner, och därför färre elektronenerginivåer, än större kristaller gör. Eftersom den totala möjliga elektronenergin för ett element förblir densamma, oavsett storlek, mindre kristaller har större avstånd mellan sina elektronenerginivåer än större kristaller.
Enligt Anderson, detta stora elektroniska energinivåavstånd bör utgöra ett problem, och han förväntade sig att supraledning skulle försvinna när avståndet blir större än den supraledande gapenergin. Anledningen för det här, generellt, är att en konsekvens av ökat avstånd är en minskning av potentiell energi, som stör konkurrensen mellan kinetisk och potentiell energi som är nödvändig för att supraledning ska ske.
För att undersöka vad som händer med supraledning av föremål kring Anderson -gränsen, forskarna i den nya studien förberedde stora mängder isolerade bly -nanokristaller i volym från 20 till 800 nm 3 .
Även om de inte direkt kunde mäta supraledning hos sådana små föremål, forskarna kunde mäta något som kallas paritetseffekt, som är resultatet av supraledning. När en elektron läggs till en superledare, den extra energin påverkas delvis av om det finns ett jämnt eller udda antal elektroner (pariteten), vilket beror på att elektronerna bildar Cooper -par. Om elektronerna inte bildar Cooper -par, det finns ingen paritetseffekt, indikerar ingen supraledning.
Även om paritetseffekten tidigare har observerats i stora superledare, denna studie är första gången som den har observerats hos små nanokristaller som närmar sig Anderson -gränsen. I enlighet med Andersons förutsägelser från mer än 50 år sedan, forskarna observerade paritetseffekten för större nanokristaller, men inte för de minsta nanokristaller under cirka 100 nm 3 .
Resultaten validerar inte bara Anderson -gissningen, men sträcker sig också till ett mer allmänt område, modellerna Richardson-Gaudin. Dessa modeller motsvarar den konventionella teorin om supraledning, Bardeen Cooper Schrieffer -teorin, för mycket små föremål.
"Vår experimentella demonstration av Anderson-gissningen är också en demonstration av giltigheten hos Richardson-Gaudin-modellerna, "berättade medförfattaren Hervé Aubin vid University Paris Sciences et Lettres och CNRS Phys.org . "Richardson-Gaudin-modellerna är en viktig del av teoretiska verk eftersom de kan lösas exakt och tillämpas på ett brett spektrum av system; inte bara för supraledande nanokristaller utan också för atomkärnor och kall fermionisk atommas, där protoner och neutroner, som är fermioner som elektroner, kan också bilda Cooper -par. "
På den mer praktiska sidan, forskarna förväntar sig att resultaten kommer att ha tillämpningar i framtida kvantdatorer.
"En av de mest intressanta tillämpningarna av supraledande öar är deras användning som Cooper -parlådor som används i kvantbitar, elementenheten i en hypotetisk kvantdator, "Sa Aubin." Än så länge, Cooper -parlådor som används i qubits är mycket större än Anderson -gränsen. När du har minskat storleken på Cooper -parlådan, kvantdatoringenjörer kommer så småningom att behöva hantera supraledning vid Andersons gräns. "
© 2017 Phys.org